题目内容
18. 如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.
如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.
分析 由矩形的性质得出∠C=90°,BC=AD=10cm,CD=AB=6cm,当点E与B重合时,A′C最小,此时BA′=BA=6cm,得出A′C=BC-BA′=4cm;当F与D重合时,A′C最大,此时A′D=AD=10cm,由勾股定理求出A′C的长,即可得出结果.
解答 解:∵四边形ABCD是矩形,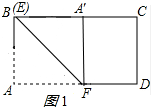
∴∠C=90°,BC=AD=10cm,CD=AB=6cm,
当点E与B重合时,A′C最小,
如图1所示:
此时BA′=BA=6cm,
∴A′C=BC-BA′=10cm-6cm=4cm;
当F与D重合时,A′C最大,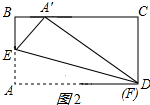
如图2所示:
此时A′D=AD=10cm,
∴A′C=$\sqrt{1{0}^{2}-{6}^{2}}$=8(cm);
综上所述:A′C的取值范围为4cm≤A′C≤8cm.
故答案为:4cm≤A′C≤8cm.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理;熟练掌握矩形和翻折变换的性质,求出A′C最小和最大时的值是解决问题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
6. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )| A. | 25° | B. | 28° | C. | 30° | D. | 32° |
7.下列调查方式合适的是( )
| A. | 对空间实验室“天空二号”零部件的检查,采用抽样调查的方式 | |
| B. | 了解炮弹的杀伤力,采用全面调查的方式 | |
| C. | 对中央台“新闻联播”收视率的调查,采用全面调查的方式 | |
| D. | 对石家庄市食品合格情况的调查,采用抽样调查的方式 |
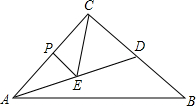 如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.