题目内容
10.将直线y=-$\frac{1}{2}$x+2先向右平移一个单位长度,再向上平移一个单位长度,所得新的直线l与x轴、y轴分别交于A、B两点,另有一条直线y=x+1.(1)求l的解析式;
(2)求点A和点B的坐标;
(3)求直线y=x+1与直线l以及y轴所围成的三角形的面积.
分析 (1)根据图象平移的规律:左加右减,上加下减,可得答案;
(2)根据自变量与函数值的对应关系,可得答案;
(3)根据解方程组,可得交点坐标,根据三角形的面积公式,可得答案.
解答 解:(1)直线y=-$\frac{1}{2}$x+2先向右平移一个单位长度,再向上平移一个单位长度得
y=-$\frac{1}{2}$(x-1)+2+1,化简得
y=-$\frac{1}{2}$x+$\frac{7}{2}$.
(2)当y=0时,0=-$\frac{1}{2}$x+$\frac{7}{2}$.解得x=7,即A(7,0);
当x=0时,y=$\frac{7}{2}$,B(0,$\frac{7}{2}$);
(3)将y=-$\frac{1}{2}$x+$\frac{7}{2}$和y=x+1联成方程组解得两直线交点为($\frac{5}{3}$,$\frac{8}{3}$).
再求出两直线与y轴交点分别为(0,$\frac{7}{2}$)和(0,1),
所以三角形面积为$\frac{1}{2}$×$\frac{5}{3}$×($\frac{7}{2}$-1)=$\frac{25}{12}$.
点评 本题考查了一次函数图象与几何变换,利用图象平移的规律是解题关键.

练习册系列答案
相关题目
1.在-4,-2,-1,0这四个数中,比-3小的数是( )
| A. | -4 | B. | -2 | C. | -1 | D. | 0 |
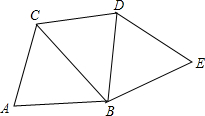 如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n. 如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.
如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为4cm≤A′C≤8cm.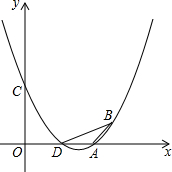 已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C. 按图填空,并注明理由.
按图填空,并注明理由.