题目内容
(1)解方程:x2+4x-3=0;
(2)解不等式组
,并把解集在数轴上表示出来.
(2)解不等式组
|
考点:解一元一次不等式组,解一元二次方程-配方法,在数轴上表示不等式的解集
专题:
分析:(1)先把常数项移到等号的右面,再在等式的两边同时加上一次项系数的一半,然后进行配方,即可得出答案;
(2)根据解不等式的步骤先求出两个不等式,然后找出公共部分,即可得出不等式组的解集,从而把解集在数轴上表示出来.
(2)根据解不等式的步骤先求出两个不等式,然后找出公共部分,即可得出不等式组的解集,从而把解集在数轴上表示出来.
解答:解:(1)x2+4x-3=0,
x2+4x=3,
x2+4x+4=3+4,
(x+2)2=7,
即 x+2=
或x+2=-
,
∴x1=
-2,x2=-
-2;
(2)
,
由①得:x≥-1,
由②得:x<3,
则原不等式组的解集是:-1≤x<3,
把不等式组的解集在数轴上表示如下:

x2+4x=3,
x2+4x+4=3+4,
(x+2)2=7,
即 x+2=
| 7 |
| 7 |
∴x1=
| 7 |
| 7 |
(2)
|
由①得:x≥-1,
由②得:x<3,
则原不等式组的解集是:-1≤x<3,
把不等式组的解集在数轴上表示如下:

点评:此题考查了配方法解一元二次方程和解不等式组,根据配方法解一元二次方程的步骤和根据不等式的性质正确解一元一次不等式组是解此题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:(1)AD平分∠BAC;(2)AE=AF.
如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:(1)AD平分∠BAC;(2)AE=AF.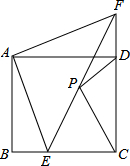 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少?
如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少?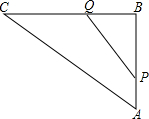 如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.
如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.