题目内容
6．已知一个圆锥的侧面积是l0πcm2，它的侧面展开图是一个圆心为144°的扇形，则这个圆锥的底面半径为（ ）| A． | $\frac{4}{5}$cm | B． | $\sqrt{5}$cm | C． | 2cm | D． | $2\sqrt{5}$cm |
分析 设圆锥的母线长为lcm，根据圆锥的侧面积为侧面展开图中扇形的面积得出$\frac{144π×{l}^{2}}{360}$=10π，求出l=5，再设圆锥的底面半径是rcm，根据圆锥的底面圆周长是扇形的弧长得出2πr=$\frac{144π×5}{180}$，解方程即可求出半径．
解答 解：设圆锥的母线长为lcm，则$\frac{144π×{l}^{2}}{360}$=10π，
解得：l=5，
设圆锥的底面半径是rcm，则2πr=$\frac{144π×5}{180}$，
解得：r=2．
即这个圆锥的底面半径为2cm，
故选C．
点评 本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．先化简，再求值（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$）÷$\frac{x}{x-2}$（其中x=3），其计算结果是（ ）
| A． | -$\frac{8}{5}$ | B． | 8 | C． | -8 | D． | $\frac{8}{5}$ |
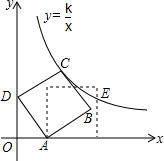如图，在平面直角坐标系中，边长为2的正方形ABCD斜靠在y轴上，点A的坐标为（1，0），反比例函数y=$\frac{k}{x}$图象经过点C，将正方形ABCD绕点A顺时针旋转一定角度后，使得点B恰好落在x轴的正半轴上，此时边BC交反比例图象于点E，则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$．
9．若a+b=1，则a2-b2+2b的值为（ ）
| A． | 4 | B． | 3 | C． | 1 | D． | 0 |
10．若a＞0且ax=2，ay=3，则ax-2y的值为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{9}$ |