题目内容
14.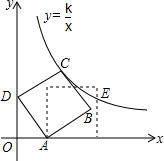 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,点A的坐标为(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$.
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,点A的坐标为(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$.
分析 先根据勾股定理求出OD的长,再过点C作CF⊥y轴于点F,根据ASA定理得出△CDF≌△DAO,故可得出C点坐标,求出k的值,再求出OH的长,进而可得出E点坐标.
解答 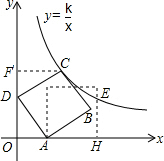 解:∵Rt△AOD中,OA=1,AD=2,
解:∵Rt△AOD中,OA=1,AD=2,
∴OD=$\sqrt{{AD}^{2}-{OA}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
过点C作CF⊥y轴于点F,
∵∠CDF+∠ADO=90°,∠CDF+∠DCF=90°,
∴∠DCF=∠ADO,
同理,∠CDF=∠DAO,
在△CDF与△DAO中,
$\left\{\begin{array}{l}∠DCF=∠ADO\\ CD=AD\\∠CDF=∠DAO\end{array}\right.$,
∴△CDF≌△DAO(ASA),
∴CF=OD=$\sqrt{3}$,DF=OA=1,
∴C($\sqrt{3}$,1+$\sqrt{3}$).
∵反比例函数y=$\frac{k}{x}$图象经过点C,
∴k=$\sqrt{3}$×(1+$\sqrt{3}$)=3+$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{3+\sqrt{3}}{x}$.
∵OH=OA+AH=1+2=3,
∴点E的横坐标为3,
∴y=$\frac{3+\sqrt{3}}{3}$=1+$\frac{\sqrt{3}}{3}$
故答案为:1+$\frac{\sqrt{3}}{3}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
5.下列事件是确定事件的是( )
| A. | 任买一张电影票,座位是偶数 | |
| B. | 在一个装有红球和白球的箱子中,任摸一个球是红色的 | |
| C. | 随意掷一枚均匀的硬币,正面朝上 | |
| D. | 三根长度分别为2cm、3cm、5cm的木棒能摆成三角形 |
2. 在⊙O中,AB是⊙O的直径,AB=8cm,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,M是AB上一动点,CM+DM的最小值是( )
在⊙O中,AB是⊙O的直径,AB=8cm,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,M是AB上一动点,CM+DM的最小值是( )
 在⊙O中,AB是⊙O的直径,AB=8cm,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,M是AB上一动点,CM+DM的最小值是( )
在⊙O中,AB是⊙O的直径,AB=8cm,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,M是AB上一动点,CM+DM的最小值是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
9.下列四个几何体中,主视图为矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.已知一个圆锥的侧面积是l0πcm2,它的侧面展开图是一个圆心为144°的扇形,则这个圆锥的底面半径为( )
| A. | $\frac{4}{5}$cm | B. | $\sqrt{5}$cm | C. | 2cm | D. | $2\sqrt{5}$cm |