题目内容
一个直角三角形的两条直角边长之比为5：12，斜边长为26，则这个直角三角形的面积为 ．
考点：一元二次方程的应用
专题：几何图形问题
分析：根据比例问题由勾股定理建立方程求出两直角边的长度，再由面积公式就可以求出结论．
解答：解：设每份为x，则两直角边分别为5x，12x，由勾股定理，得
25x2+144x2=676，
解得：x1=-2（舍去），x2=2．
∴两直角边分别为：10，24．
∴直角三角形的面积为：
×10×24=120．
故答案为：120
25x2+144x2=676，
解得：x1=-2（舍去），x2=2．
∴两直角边分别为：10，24．
∴直角三角形的面积为：
| 1 |
| 2 |
故答案为：120
点评：本题考查了列一元二次方程解实际问题的运用，一元二次方程的解法的运用，勾股定理的运用，三角形的面积公式的运用，解答时求出直角三角形的边长是关键．
练习册系列答案
相关题目
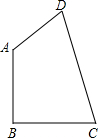如图，在四边形ABCD中，AB，BC，CD，DA的长分别为2，2，
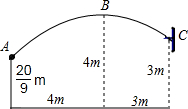如图，一场篮球赛中，球员甲跳起投篮，已知球出手时离地面
如图，已知在△ABC和△DEF中，如果AB=DE，BC=EF，只要找出∠
如图，纵截面是一等腰梯形的拦水坝，两腰与上底的和为4m，底角为60°，当坝高为