题目内容
8. 如图,△ABC中,D是AB中点,P为BC延长线上一点,且∠CAP=∠B,DP与AC交于E点,求证:$\frac{P{A}^{2}}{P{C}^{2}}$=$\frac{AE}{EC}$.
如图,△ABC中,D是AB中点,P为BC延长线上一点,且∠CAP=∠B,DP与AC交于E点,求证:$\frac{P{A}^{2}}{P{C}^{2}}$=$\frac{AE}{EC}$.
分析 过C作CF∥AB交PD于F,如图,先证明△PAC∽△PBA得到PA2=PC•PB,再证明△ADE∽△CHE得到$\frac{AE}{EC}$=$\frac{AD}{CH}$,证明△PBD∽△PCH得到$\frac{BD}{CH}$=$\frac{PB}{PC}$,利用AD=BD得到$\frac{AE}{EC}$=$\frac{PB}{PC}$,从而有$\frac{P{A}^{2}}{P{C}^{2}}$=$\frac{AE}{EC}$.
解答 证明:过C作CF∥AB交PD于F,如图,
∵∠CAP=∠B,∠APC=∠BPA,
∴△PAC∽△PBA,
∴$\frac{PA}{PB}$=$\frac{PC}{PA}$,即PA2=PC•PB,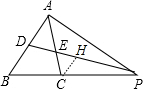
∴$\frac{P{A}^{2}}{P{C}^{2}}$=$\frac{PC•PB}{P{C}^{2}}$=$\frac{PB}{PC}$,
∵CH∥AD,
∴△ADE∽△CHE,
∴$\frac{AE}{EC}$=$\frac{AD}{CH}$,
∵CH∥BD,
∴△PBD∽△PCH,
∴$\frac{BD}{CH}$=$\frac{PB}{PC}$,
而AD=BD,
∴$\frac{AE}{EC}$=$\frac{PB}{PC}$,
∴$\frac{P{A}^{2}}{P{C}^{2}}$=$\frac{AE}{EC}$.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;再利用相似三角形的性质时,主要得到相似比和对应角相等.解决本题的关键是过C作CF∥AB交PD于F,从而构建相似三角形.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
13. 利用图中图形面积关系可以解释的公式是( )
利用图中图形面积关系可以解释的公式是( )
 利用图中图形面积关系可以解释的公式是( )
利用图中图形面积关系可以解释的公式是( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)(a-b)=a2-b2 | D. | (a+b)(a2-ab+b3)=a3+b3 |
18.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
(2)用含x的代数式表示运送甲仓库100吨水泥的运费为-10x+15000元.(写出化简后的结果)
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
 如表给出一个二次函数的一些取值情况:
如表给出一个二次函数的一些取值情况: