Question

7．已知在△ABC中，AB=1，BC=4$\sqrt{\frac{1}{2}}$，CA=$\frac{1}{5}$$\sqrt{125}$．
（1）分别化简4$\sqrt{\frac{1}{2}}$，$\frac{1}{5}$$\sqrt{125}$的值．
（2）试在4×4的方格纸上画出△ABC，使它的顶点都在方格的顶点上（每个小方格的边长为1）．
（3）求出△ABC的面积．

Answer 1

分析 （1）首先化简$\sqrt{\frac{1}{2}}$和$\sqrt{125}$，再分别计算乘法即可；
（2）根据勾股定理画出AC=$\sqrt{5}$，再确定B的位置，既要使AB=1，又要使BC=$2\sqrt{2}$即可；
（3）利用三角形的面积公式，以BA为底，确定AB上的高为2，再计算即可．

解答 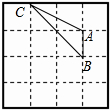解：（1）4$\sqrt{\frac{1}{2}}$=4×$\sqrt{\frac{1×2}{2×2}}$=2$\sqrt{2}$，
$\frac{1}{5}$$\sqrt{125}$=$\frac{1}{5}$×$\sqrt{25×5}$=$\frac{1}{5}$×$5\sqrt{5}$=$\sqrt{5}$；

（2）如图所示：

（3）△ABC的面积$\frac{1}{2}×$1×2=1平方单位．

点评 此题主要考查了应用与设计作图，以及勾股定理的应用和二次根式的计算，关键是正确化简AC、BC的长．