题目内容
2.观察下面的几个算式,你发现了什么规律?①16×14=224=1×(1+1)×100+6×4=224
②23×27=621=2×(2+1)×100+3×7=621
③32×38=1216=3×(3+1)×100+2×8=1216
…
(1)上面的规律,迅速写出答案.
64×66=4224
73×77=5621
81×89=7209
(2)设两个两位数分别是(10n+a)、(10n+b),其中a+b=10),请你利用所学知识证明上面所发现的规律.
分析 (1)规律:两个因数都是两位数,其中十位数字相同,个位数字的和为10,它们的积为:十位数字×(十位数字+1)×100+两个个位数字的积.
(2)将(1)中的数字换成字母按照多项式乘法验证即可.
解答 解:(1)64×66=6×(6+1)×100+4×6=4224,
73×77=7×(7+1)×100+3×7=5621,
81×89=8×(8+1)×100+1×9=7209,
故答案为:4224,5621,7209;
(2)发现的规律为:(10n+a)•(10n+b)=100n(n+1)+ab,
证明:∵a+b=10,
∴等式左边=100n2+10bn+10an+ab=100n2+10n(a+b)+ab=100n2+100n+ab,
右边=100n2+100n+ab,
∴左边=右边,
则(10n+a)•(10n+b)=100n(n+1)+ab.
点评 本题考查了数字的变化规律及整式的运算,解题的关键是观察题意得出规律,并熟练掌握整式的混合运算.

练习册系列答案
相关题目
13.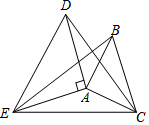 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
①BE=DC②AD∥BC③BE=DE④BE=EC.
 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )①BE=DC②AD∥BC③BE=DE④BE=EC.
| A. | ①③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
17.已知反比例函数y=$\frac{5}{x}$,当1<x≤4时,y的最大整数值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
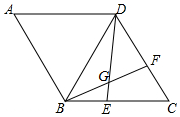 如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.
如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.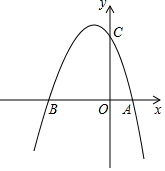 如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3).
如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3). 如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)
如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)