题目内容
17.加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可为完成1200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一,第二工序所完成的件数相等.(列二元一次方程)分析 由题意可得等量关系:每天第一、第二道工序所完成的件数相等和现有7位工人参加这两道工序,得出方程组,求出即可.
解答 解:设第一道工序需要x人,则第二道工序需要y人,
根据题意列方程组得:$\left\{\begin{array}{l}{900x=1200y}\\{x+y=7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$.
答:第一道工序需要4人,则第二道工序需要3人.
点评 此题主要考查了二元一次方程组的应用,根据题意得出利用总人数和两道工序件数相等得出等式是解题关键.

练习册系列答案
相关题目
1.在△ABC中,两中线AD与CF相交于点G,若∠AFC=45°,∠AGC=60°,则∠ACF的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
5.王老师要选择两名同学担任九年级毕业典礼主持人.现有2名男同学和3名女同学候选,那么王老师选择一名男同学和一名女同学担任主持人的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |
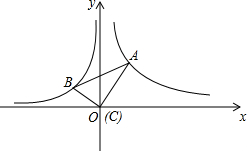 如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.
如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.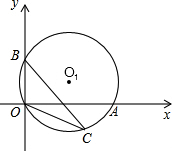 如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.
如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.