题目内容
1.在△ABC中,两中线AD与CF相交于点G,若∠AFC=45°,∠AGC=60°,则∠ACF的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 首先由重心的性质得$\frac{CG}{GF}$=2,作CE⊥AG于点E,连接EF,易得∠ECG=30°,得GE=GF,∠FGE=120°,那么∠GFE=∠FEG=30°,EF=EC,由∠EFA=45°-30°=15°,∠FAD=∠AGC-∠AFC=15°,得AE=EC,由等腰直角三角形的性质得∠ACE=45°,得∠ACF的度数.
解答 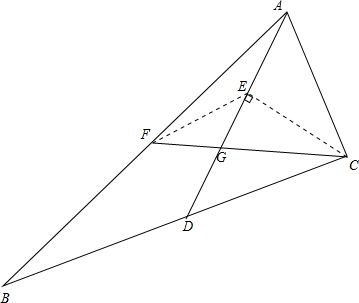 解:∵点G是△ABC的重心,
解:∵点G是△ABC的重心,
∴$\frac{CG}{GF}$=2,
作CE⊥AG于点E,连接EF,
∴△CEG是直角三角形,
∵∠EGC=60°,
∴∠ECG=30°,
那么EG=$\frac{1}{2}$CG=GF,
∴GE=GF,
∠FGE=120°,
∴∠GFE=∠FEG=30°,
而∠ECG=30°,
∴EF=EC,
∵∠EFA=45°-30°=15°,
∠FAD=∠AGC-∠AFC=15°,
∴∠FAD=∠EFA,
∴EF=AE,
∴AE=EC,
∵△AEC是等腰直角三角形,
∴∠ACE=45°,
∴∠ACF=∠ACE+∠ECF=30°+45°=75°,
故选D.
点评 本题主要考查了重心的性质,含30°角直角三角形的性质,等腰三角形的性质等,作出恰当的辅助线是解答此题的关键.

练习册系列答案
相关题目
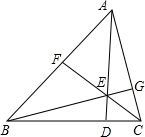 如图,在△ABC中,AD、BG、CF交于点E,则$\frac{EF}{CF}$+$\frac{EG}{BG}$+$\frac{ED}{AD}$=1.
如图,在△ABC中,AD、BG、CF交于点E,则$\frac{EF}{CF}$+$\frac{EG}{BG}$+$\frac{ED}{AD}$=1.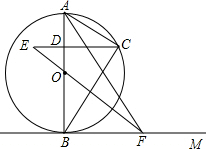 如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中保持OF∥AC.
如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中保持OF∥AC.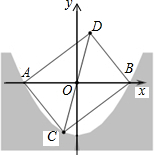 某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2-4.
某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2-4.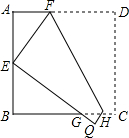 如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是12cm.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是12cm.