题目内容
8.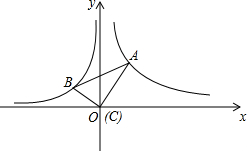 如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.
如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.
分析 过A作AE⊥x轴于E过B作BF⊥x轴于F,通过△AOE∽△BOF,得到$\frac{AE}{OF}=\frac{OE}{BF}=\frac{AO}{BO}$,设A(m,$\frac{3}{m}$),于是得到AE=$\frac{3}{m}$,OE=m,从而得到B(-$\frac{\sqrt{3}}{m}$,$\frac{\sqrt{3}m}{3}$),于是求得结果.
解答 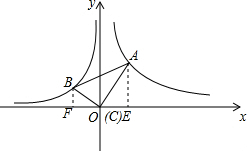 解:过A作AE⊥x轴于E过B作BF⊥x轴于F,
解:过A作AE⊥x轴于E过B作BF⊥x轴于F,
∵∠AOC=90°∠A=30°,
∴∠OAE+∠AOE=∠AOE+∠BOF=90°,
∴△AOE∽△BOF,
∴$\frac{AE}{OF}=\frac{OE}{BF}=\frac{AO}{BO}$,
设A(m,$\frac{3}{m}$),
∴AE=$\frac{3}{m}$,OE=m,
∵$\frac{AO}{OB}=\sqrt{3}$,
∴OF=$\frac{\sqrt{3}}{m}$,OE=$\frac{\sqrt{3}m}{3}$,
∴B(-$\frac{\sqrt{3}}{m}$,$\frac{\sqrt{3}m}{3}$),
∴k=-$\frac{\sqrt{3}}{m}$$•\frac{\sqrt{3}m}{3}$=1.
故答案为:1.
点评 本题考查了相似三角形的判定和性质,反比例函数图象上点的坐标特征,三角函数,作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
17.同时抛掷两枚质地均匀的正方体,正方体的六个面上分别刻有1到6的整数,下列事件是不可能事件的是( )
| A. | 点数之和为13 | B. | 点数之和小于3 | ||
| C. | 点数之和大于4且小于8 | D. | 点数之和为12 |
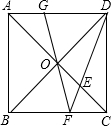 如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.
如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.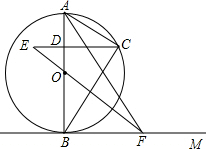 如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中保持OF∥AC.
如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中保持OF∥AC.