题目内容
9.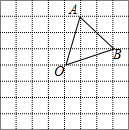 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).(1)画出△AOB绕点O逆时针旋转180°后得到△A′OB′;
(2)点A关于点O中心对称的点A′的坐标为(-1,-3);
(3)连接AB′、BA′,四边形ABA′B′是什么四边形:矩形.
分析 (1)根据中心旋转图形的定义画出图形即可.
(2)由点A′的位置可以写出点A′坐标.
(3)结论是矩形,根据对角线相等的平行四边形是矩形进行证明.
解答 解:(1)△AOB绕点O逆时针旋转180°后得到△A′OB′的图象如图所示: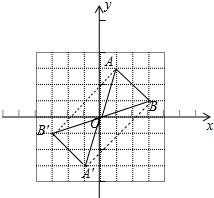
(2)由图象可知点A′坐标(-1,-3).
故答案为(-1,-3).
(3)连接AB′、BA′,∵OA=OA′,OB=OB′,
∴四边形AB′A′B是平行四边形,
∵OA=OB,
∴AA′=BB′,
∴四边形AB′A′B是矩形.
故答案为矩形.
点评 本题考查旋转变换、中心对称的定义、矩形的判定、点与坐标的关系等知识,正确画出中心旋转图形是解题的关键,记住矩形的3种判定方法,属于中考常考题型.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
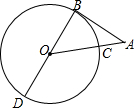 如图,BD为⊙O的直径,AB与⊙O相切于点B,连结AO,AO与⊙O交于点C,若∠A=40°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{13}{9}$π.
如图,BD为⊙O的直径,AB与⊙O相切于点B,连结AO,AO与⊙O交于点C,若∠A=40°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{13}{9}$π.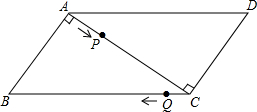 已知,如图,用两块一样大的直角三角板拼成一个平行四边形,∠BAC=∠ACD=90°.在?ABCD中,AB=3cm,BC=5cm,点P自A向C、沿AC的方向匀速运动,速度为1cm/s;同时,点Q从点C出发,自C向B、沿CB方向匀速运动,速度为1cm/s;过点P作PM⊥AD,并与AD相交于点M,当P、Q中有一个点到达终点时,另一个点也停止运动.设运动时间为t(s).解答下列问题:
已知,如图,用两块一样大的直角三角板拼成一个平行四边形,∠BAC=∠ACD=90°.在?ABCD中,AB=3cm,BC=5cm,点P自A向C、沿AC的方向匀速运动,速度为1cm/s;同时,点Q从点C出发,自C向B、沿CB方向匀速运动,速度为1cm/s;过点P作PM⊥AD,并与AD相交于点M,当P、Q中有一个点到达终点时,另一个点也停止运动.设运动时间为t(s).解答下列问题: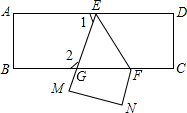 如图,把一张长方形纸片ABCD沿EF折叠,折叠后点D与M点重合,点C与点N重合,EM与BC相交于点G,若∠AEM=52°,则∠EFG=64°.
如图,把一张长方形纸片ABCD沿EF折叠,折叠后点D与M点重合,点C与点N重合,EM与BC相交于点G,若∠AEM=52°,则∠EFG=64°.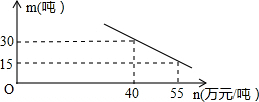 某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.
某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.