题目内容
19.现有三个正整数,其中每一个都小于2000,而其中每两个数的最小公倍数都大于2000.证明:这些数的倒数之和小于2.分析 先根据每两个数的最小公倍数都大于2000,每一个都小于2000得到这三个数大于等于2,再根据倒数的定义得到$\frac{1}{a}$≤$\frac{1}{2}$,$\frac{1}{b}$≤$\frac{1}{2}$,$\frac{1}{c}$≤$\frac{1}{2}$,依此即可求解.
解答 证明:∵每两个数的最小公倍数都大于2000,每一个都小于2000,
∴这三个正整数没有1,即这三个数大于等于2,
设这三个数是a,b,c,
则$\frac{1}{a}$≤$\frac{1}{2}$,$\frac{1}{b}$≤$\frac{1}{2}$,$\frac{1}{c}$≤$\frac{1}{2}$,
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≤$\frac{3}{2}$<2.
点评 考查了约数与倍数,根据题意得到这三个数大于等于2是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7.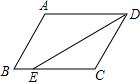 如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )
如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )
 如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )
如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
 如图,∠1=∠ACB,∠2=∠3,证明:CD∥FH.
如图,∠1=∠ACB,∠2=∠3,证明:CD∥FH.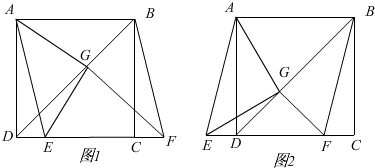
 已知:如图?ABCD中,DM=BN,BE=DF,求证:四边形MENF是平行四边形.
已知:如图?ABCD中,DM=BN,BE=DF,求证:四边形MENF是平行四边形.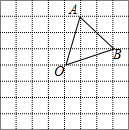 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).