题目内容
 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.(1)在图中画出线段CD,使∠DCB=∠ACB(点D在小正方形的格点上)
(2)连接BD,请直接写出四边形ABDC的面积.
考点:作图—应用与设计作图,角平分线的性质
专题:
分析:(1)根据角平分线的作法作∠DCB,先以C为圆心,以AC为半径画圆,再以B为圆心,以AB为半径画圆,两圆相交于点D,连接CD,则∠DCB即为所求角;
(2)根据△ACB≌△DCB可知S四边形ABDC=2S△ABC,由此可得出结论.
(2)根据△ACB≌△DCB可知S四边形ABDC=2S△ABC,由此可得出结论.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)由作图可知△ACB≌△DCB,
则S四边形ABDC=2S△ABC=2×
×2×4=4.
 解:(1)如图所示;
解:(1)如图所示;(2)由作图可知△ACB≌△DCB,
则S四边形ABDC=2S△ABC=2×
| 1 |
| 2 |
点评:本题考查的是作图-应用与设计作图,熟知角平分线的作法是解答此题的关键.

练习册系列答案
相关题目
如图,下列“回形”图形中,水平方向的间隔和竖直方向的间隔都是1,其中,第(1)个图形中从A到B1
的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

| A、132 | B、156 |
| C、182 | D、210 |
在时刻9:30时,时钟上的时针与分针间的夹角是( )
| A、75° | B、90° |
| C、105° | D、120° |
二次函数y=ax2+bx+c(a≠0)的图象过点(-4,3),(-5,-3)和(0,-13),则下列各点,该二次函数的图象不经过的是( )
| A、(-1,-3) |
| B、(-2,-3) |
| C、(1,-27) |
| D、(-6,-13) |
下列变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
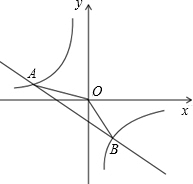 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.
某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.