题目内容
 已知:抛物线C1:y=-
已知:抛物线C1:y=-
| ||
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
| A、向左平移3个单位 | ||||
| B、向右平移6个单位 | ||||
C、向右平移
| ||||
| D、向左平移6个单位 |
考点:二次函数图象与几何变换
专题:
分析:根据关于y轴对称的点的坐标特征求得抛物线为C2的顶点坐标,通过对比抛物线为C2与C1的顶点坐标可以得到答案.
解答:解:∵y=-
x2+2
x-
=-
(x-3)2+
,
∴抛物线为C1的顶点坐标是(3,
).
根据题意知,抛物线C1与抛物线为C2关于y轴对称,则抛物线C2的顶点坐标是(-3,
).
∴由点(3,
)向左平移6个单位得到(-3,
),
即把C1向左平移6个单位可得到C2.
故选:D.
| ||
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
| ||
| 3 |
| 4 |
| 3 |
| 3 |
∴抛物线为C1的顶点坐标是(3,
| 4 |
| 3 |
| 3 |
根据题意知,抛物线C1与抛物线为C2关于y轴对称,则抛物线C2的顶点坐标是(-3,
| 4 |
| 3 |
| 3 |
∴由点(3,
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
即把C1向左平移6个单位可得到C2.
故选:D.
点评:本题考查了二次函数图象与几何变换.根据题意得到两个抛物线关于y轴对称是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
二次函数y=ax2+bx+c(a≠0)的图象过点(-4,3),(-5,-3)和(0,-13),则下列各点,该二次函数的图象不经过的是( )
| A、(-1,-3) |
| B、(-2,-3) |
| C、(1,-27) |
| D、(-6,-13) |
下列判断正确的是( )
| A、“昨晚下了雨”是随机事件 |
| B、明天买彩票可能会中大奖 |
| C、连续抛硬币2次,必有一次正面朝上 |
| D、在只装红球的袋中可能会摸出白球 |
 如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )| A、AE=BE |
| B、CE=DE |
| C、弧AC=弧BC |
| D、弧AD=弧BD |
下列变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列计算正确的是( )
| A、3a+5b=5ab |
| B、5y-3y=2 |
| C、7+a=7a |
| D、3x2y-2yx2=x2y |
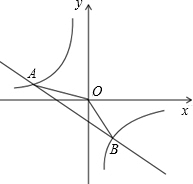 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=
 如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.