题目内容
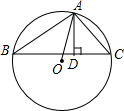 如图,已知△ABC内接于⊙O,AD为BC边上的高.
如图,已知△ABC内接于⊙O,AD为BC边上的高.(1)试写出AB,AC,AD与半径r之间的关系并证明;
(2)如果作∠BAC的角平分线交⊙O于M,那么AM是否是∠OAD的角平分线?说明理由.
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图,延长AO,交⊙O于点E,连接EC;证明△ABD∽△AEC,得到AB•AC=2r•AD.
(2)证明∠BAD=∠EAC,进而得到∠BAE=∠CAD,即可解决问题.
(2)证明∠BAD=∠EAC,进而得到∠BAE=∠CAD,即可解决问题.
解答: 解:(1)如图,延长AO,交⊙O于点E,连接CE;
解:(1)如图,延长AO,交⊙O于点E,连接CE;
∵AD⊥BC,AE为⊙O的直径,
∴∠ADB=∠ACE,而∠B=∠E,
∴△ABD∽△AEC,
∴AB:AE=AD:AC;设⊙O的半径为r,
∴AB•AC=2r•AD.
(2)∵△ABD∽△AEC,
∴∠BAD=∠EAC,
∴∠BAE=∠CAD,
∴若AM平分∠BAC,则AM一定平分∠OAD.
 解:(1)如图,延长AO,交⊙O于点E,连接CE;
解:(1)如图,延长AO,交⊙O于点E,连接CE;∵AD⊥BC,AE为⊙O的直径,
∴∠ADB=∠ACE,而∠B=∠E,
∴△ABD∽△AEC,
∴AB:AE=AD:AC;设⊙O的半径为r,
∴AB•AC=2r•AD.
(2)∵△ABD∽△AEC,
∴∠BAD=∠EAC,
∴∠BAE=∠CAD,
∴若AM平分∠BAC,则AM一定平分∠OAD.
点评:该题以圆为载体,以圆周角定理及其推论、相似三角形的判定及其性质的考查为核心构造而成的一道综合性几何题;解题的关键是作辅助线,构造相似三角形.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
如图,下列“回形”图形中,水平方向的间隔和竖直方向的间隔都是1,其中,第(1)个图形中从A到B1
的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

| A、132 | B、156 |
| C、182 | D、210 |
平面内有五个点,过每两个点作一条直线,可以作几条直线?( )
| A、1条、4条、8条或10条 |
| B、1条、5条、9条或10条 |
| C、1条、5条、8条或10条 |
| D、1条或10条 |
 如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )| A、AE=BE |
| B、CE=DE |
| C、弧AC=弧BC |
| D、弧AD=弧BD |
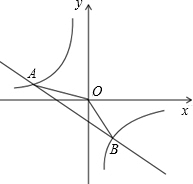 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.
某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.