题目内容
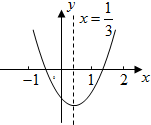 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:①abc>0;②a-b+c>0;③2a-3b=0;④b2-4ac>0,
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:①由抛物线的开口向上知a>0,
由抛物线与y轴的交点为在y轴的负半轴上,可推出c<0,
由图可知对称轴为x=-
>0,可推出b<0,
所以abc>0,故①正确;
②把x=-1时可以看出,y>0,所以a-b+c>0,
故②正确.
③对称轴x=-
=
,
∴3b=-2a,
∴2a+3b=0,
∴③是错误的;
④∵抛物线与x轴有两个交点,
∴b2-4ac>0,
故④正确.
所以正确的有①②④共3个.
故选:C.
由抛物线与y轴的交点为在y轴的负半轴上,可推出c<0,
由图可知对称轴为x=-
| b |
| 2a |
所以abc>0,故①正确;
②把x=-1时可以看出,y>0,所以a-b+c>0,
故②正确.
③对称轴x=-
| b |
| 2a |
| 1 |
| 3 |
∴3b=-2a,
∴2a+3b=0,
∴③是错误的;
④∵抛物线与x轴有两个交点,
∴b2-4ac>0,
故④正确.
所以正确的有①②④共3个.
故选:C.
点评:本题考查了二次函数y=ax2+bx+c系数符号的确定物线开口方向、对称轴和抛物线与y轴的交点确定,解题时要注意数形结合的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,下列“回形”图形中,水平方向的间隔和竖直方向的间隔都是1,其中,第(1)个图形中从A到B1
的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

的折线长为6,第(2)个图形中从A到B2的折线长为20,第(3)个图形中从A到B3的折线长为42,…,按此规律,则第(6)个图形中从A到B6的折线长为( )

| A、132 | B、156 |
| C、182 | D、210 |
在时刻9:30时,时钟上的时针与分针间的夹角是( )
| A、75° | B、90° |
| C、105° | D、120° |
下列判断正确的是( )
| A、“昨晚下了雨”是随机事件 |
| B、明天买彩票可能会中大奖 |
| C、连续抛硬币2次,必有一次正面朝上 |
| D、在只装红球的袋中可能会摸出白球 |
 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为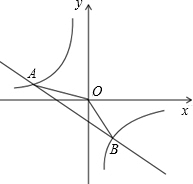 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=