题目内容
8.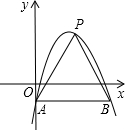 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
分析 首先求得A的坐标,则B的纵坐标即可求得,进而求得B的坐标,求得AB的长,确定二次函数的顶点坐标,在△PAB的面积的最大值即可求得,进而求得三角形面积的范围.
解答 解:y=-(x-2)2+3中令x=0,则y=-4+3=-1,
则A的坐标是(0,-1),
在y=-(x-2)2+3中令y=-1,解得x=0或4,则B的坐标是(4,-1).
则AB=4.
∵y=-(x-2)2+3的顶点坐标是(2,3),到AB的距离是4.
∴△PAB的面积的最大值是$\frac{1}{2}$×4×4=8.
则S的范围是0<S≤8.
故答案是:0<S≤8.
点评 本题考查了二次函数的图象与三角形的面积,函数图象与x轴、y轴交点的求法,求与x轴交点时令y=0求得横坐标,求与y轴的交点时令x=0求纵坐标.

练习册系列答案
相关题目
15.计算:a$\sqrt{b}$-c$\sqrt{b}$的结果是( )
| A. | a-c | B. | (a-c)$\sqrt{b}$ | C. | $\sqrt{{a}^{2}b}$-$\sqrt{{c}^{2}b}$ | D. | a-c$\sqrt{b}$ |
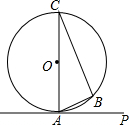 如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.
如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.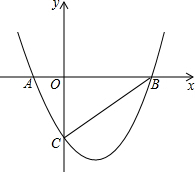 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.
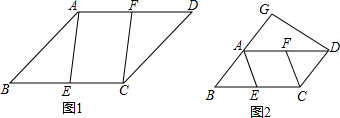
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.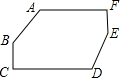 如图,已知AF∥CD,∠A=∠D,∠B=∠E.
如图,已知AF∥CD,∠A=∠D,∠B=∠E.