题目内容
13．
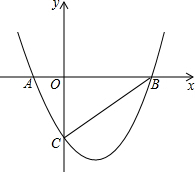如图，抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B，与y轴相交于点C，连接BC，在抛物线上找点D，连接CD，若∠BCD=90°，求点D的坐标．
分析 先计算自变量为0时的函数值得到C点坐标，通过解方程$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=0得到B点坐标，再把CB绕点C顺时针旋转90°得到CB′，如图，则B′（$\sqrt{3}$，-2-$\sqrt{3}$），利用待定系数法可求出直线CB′的解析式，然后解方程$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$可求出D点坐标．
解答 解：当x=0时，y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=-$\sqrt{3}$，则C（0，-$\sqrt{3}$），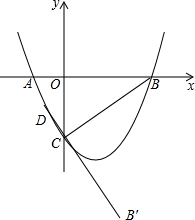
当y=0时，$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=0，解得x1=-1，x2=2，则A（-1，0），B（2，0），
把CB绕点C顺时针旋转90°得到CB′，如图，则B′（$\sqrt{3}$，-2-$\sqrt{3}$），
直线CB′交抛物线于点D，
设直线CB′的解析式为y=kx-$\sqrt{3}$，
把B′（$\sqrt{3}$，-2-$\sqrt{3}$）代入得$\sqrt{3}$k-$\sqrt{3}$=-2-$\sqrt{3}$，解得k=-$\frac{2\sqrt{3}}{3}$，
所以直线CB′的解析式为y=-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$，
解方程$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$，解得x1=0，x2=-$\frac{1}{3}$，
当x=-$\frac{1}{3}$时，y=-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$=-$\frac{7\sqrt{3}}{9}$，
所以D点坐标为（-$\frac{1}{3}$，-$\frac{7\sqrt{3}}{9}$）．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．解决本题的关键是通过旋转确定B′坐标，从而得到直线CD的解析式．
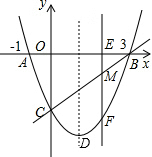如图，抛物线与x轴交于点A（-1，0）、点B（3，0），交y轴于点C（0，-3），点M为线段BC上一动点，过点M作x轴的垂线，交x轴于点E，交抛物线于点F
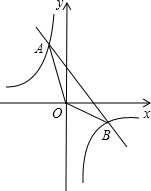如图，一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A（-1，3），B（3，a）两点．
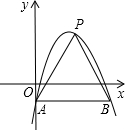如图，在平面直角坐标系中，抛物线y=-（x-2）2+3与y轴交于点A，过点A与x轴平行的直线交抛物线于另一点B．点P是直线AB上方的抛物线上一点，设点P的横坐标为m，则△PAB的面积S的取值范围为0＜S≤8．
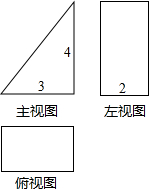一几何体的三视图如图所示，求该几何体的表面积．
已知二次函数y=ax2+bx+c的图象如图所示，记m=|a-b+c|+|2a+b+c|，n=|a+b+c|+|2a-b-c|．抛物线与x轴的其中一个交点1＜x2＜3，试比较m与n的大小，并说明理由．