题目内容
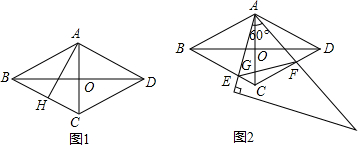
15.在平行四边形ABCD中,点E、F分别为边BC、AD的中点,连接AE、CF.(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,过点D作DG⊥AB,垂足为点G,若AG=AB,在不添加任何辅助线的情况下,请直接写出图2中所有与CF相等的线段.
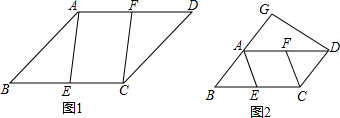
分析 (1)如图1中,欲证明四边形AECF是平行四边形只要证明AF=EC,AF∥EC即可.
(2)如图2中,结论:与CF相等的线段有:AF,DF,AE,BE.EC.先证明四边形ACDG是矩形,再证明四边形AECF是矩形即可解决问题.
解答 (1)证明:如图1中,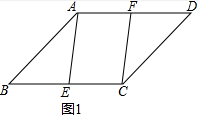 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AF=$\frac{1}{2}$AD,EC=$\frac{1}{2}$BC,
∴AF=EC.AF∥EC,
∴四边形AECF是平行四边形.
(2)与CF相等的线段有:AF,DF,AE,BE.EC.
理由: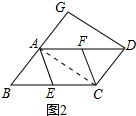 如图2中,连接AC.
如图2中,连接AC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=AG,
∴AG=CD,AG∥CD,
∴四边形ACDG是平行四边形,
∵∠G=90°,
∴四边形ACDG是矩形,
∴∠ACD=90°,∵AF=DF,
∴AF=CF=DF,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
∴CF=AF=DF=AE=EC=BE.
点评 本题考查平行四边形的性质和判定、矩形的判定和性质、菱形的判定和性质等知识,解题的关键是熟练掌握这些知识,灵活运用这些知识解决问题,所以中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.15的负的平方根介于( )
| A. | -4与-3之间 | B. | -5与-4之间 | C. | -3与-2之间 | D. | -2与-1之间 |
4.下列各数中,不是无理数的是( )
| A. | $\sqrt{7}$ | B. | $\frac{22}{7}$ | C. | $\frac{π}{2}$ | D. | 0.151151115… |
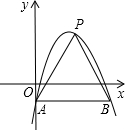 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.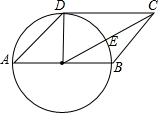 如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.
如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.