题目内容
16.轮船在海面上以每小时15海里的速度向正北方向航行,上午8时到达A处,测得灯塔C在北偏西45°方向;上午10时到达B处,又侧得灯塔C在北偏西60°方向.(1)根据题设条件,选用适当的比例尺画出图形;
(2)量出BC的图上距离,并推算出BC的实际距离;轮船继续向北航行到达D处,这时灯塔C在轮船的正西方向,这时CD的实际距离是多少?
(3)你能确定轮船到达D处时的时间吗?
分析 (1)用1cm表示10海里,根据题意画出图形即可;
(2)量出BC=3cm,推算出BC的实际距离,然后解直角三角形求得CD的实际距离;
(3)根据CD 的长度即可确定轮船到达D处时的时间.
解答 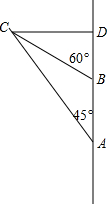 解:(1)用1cm表示10海里,如图所示;
解:(1)用1cm表示10海里,如图所示;
(2)量得BC=3cm,
∵AB=15×2=30(海里),∠CAB=45°,∠CBD=60°,
∴CD=AD,BD=$\frac{CD}{tan60°}$=$\frac{CD}{\sqrt{3}}$,
∵AB=AD-BD=CD-$\frac{CD}{\sqrt{3}}$=30,
∴CD=15(3+$\sqrt{3}$)海里.
答:CD的实际距离为15(3+$\sqrt{3}$)海里;
(3)能,
∵BD=$\frac{CD}{tan60°}$=15($\sqrt{3}+$1),
∴15($\sqrt{3}+$1)÷15=($\sqrt{3}+$1)≈2.7小时,
∴轮船到达D处时的时间12时42分.
点评 本题考查了解直角三角形的应用-方向角问题,等腰三角形的性质和判定,三角形的外角性质,关键是准确画出图形,求出∠C=∠CAB,题目比较典型,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,第二次取出的数字记为
,第二次取出的数字记为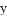 ,求两次抽到数字组成的点(x,y)在直线
,求两次抽到数字组成的点(x,y)在直线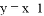 上的概率。
上的概率。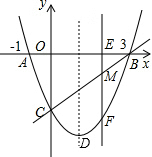 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F 如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.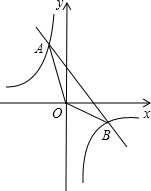 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.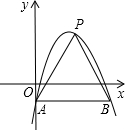 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.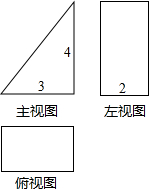 一几何体的三视图如图所示,求该几何体的表面积.
一几何体的三视图如图所示,求该几何体的表面积.