题目内容
19.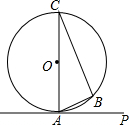 如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.
如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.(1)当AC是直径时,∠C与∠BAP的大小关系如何?
(2)当AC不是直径时,(1)题的关系还存在吗?试说明你的理由.
分析 (1)根据切线的性质得出∠CAB+∠BAP=90°,再利用直径得出∠ACB+∠CAB=90°证明即可;
(2)连接AO并延长交圆于E,连接BE,根据直径所对的圆周角是直角,可以得到∠E+∠EAB=90°;再根据AB是切线可以得到∠EAB+∠1=90°,所以∠E=∠1,最后根据等弧所对的圆周角相等就可以的得到所要的结论.
解答 解:(1)∠C=∠BAP,理由如下:
∵PA是⊙O的切线,切点为A,
∴∠CAP=90°,
∴∠CAB+∠BAP=90°,
∵AC是直径,
∴∠ACB+∠CAB=90°,
∴∠C=∠BAP;
(2)如图,作直径AE,连接EB,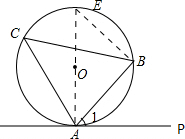
∠C=∠BAP
∵AE是⊙O的直径,
∴∠EAB+∠E=∠EBA=90°;
又∵AB是⊙O的切线,
∴∠EAB+∠1=90°,
∴∠1=∠E;
∴∠C=∠1.
∴∠C=∠BAP.
点评 本题综合运用了切线的性质、等角的余角相等以及圆周角定理的推论,熟记定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
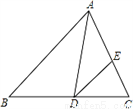
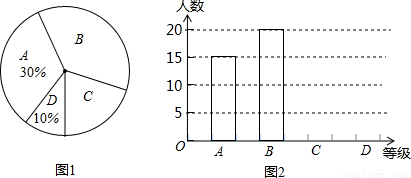
 如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.
如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.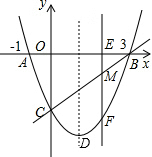 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F 如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.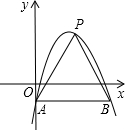 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.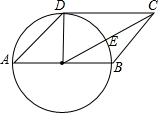 如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.
如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.