题目内容
3.在实数范围内分解因式(1)x2-2
(2)x2-2$\sqrt{3}$x+3
(3)x5-9x
(4)a4-3a2+2.
分析 (1)直接利用平方差公式分解因式.平方差公式:a2-b2=(a+b)(a-b);
(2)利用完全平方公式分解因式,完全平方公式:(a±b)2=a2±2ab+b2;
(3)先提取公因式x,再利用平方差公式分解,注意要分解彻底;
(4)先用十字相乘法分解,再用平方差公式分解因式.
解答 解:(1)原式=x2-($\sqrt{2}$)2=(x+$\sqrt{2}$)(x-$\sqrt{2}$);
(2)原式=x2-2•x•$\sqrt{3}$+($\sqrt{3}$)2=(x-$\sqrt{3}$)2;
(3)原式=x(x4-9)
=x(x2+3)(x2-3)
=x(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$);
(4)原式=(a2-1)(a2-2)
=(a+1)(a-1)(a+$\sqrt{2}$)(a-$\sqrt{2}$).
点评 本题主要考查实数范围内分解因式能力,当一个多项式有公因式,将其分解因式时应先提取公因式,再对余下的多项式继续分解.当要求在实数范围内进行因式分解时,分解的式子的结果一般要分到出现无理数为止.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
10.15的负的平方根介于( )
| A. | -4与-3之间 | B. | -5与-4之间 | C. | -3与-2之间 | D. | -2与-1之间 |
 ,DE=10,则BC等于( )
,DE=10,则BC等于( )
 如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm.
如图,△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=15cm,BC=20cm,CA=25cm. 如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.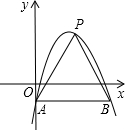 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.