题目内容
12.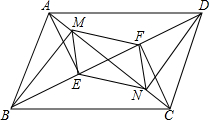 如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.
如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.
分析 证明ABM≌△CDN证得AM=CN,可以证得OM=ON,同法证得OE=OF,根据对角线互相平分的四边形是平行四边形即可证得.
解答 证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AB∥CD,
∴∠BAM=∠DCN,
又∵BM⊥AC,DN⊥AC,
∴∠AMB=∠DNC=90°,
∴△ABM和△CDN中,
$\left\{\begin{array}{l}{∠BAM=∠DCN}\\{AB=CD}\\{∠AMB=∠DNC}\end{array}\right.$,
∴△ABM≌△CDN,
∴AM=CN,
又∵OA=OC,
∴OM=ON,
同理OE=OF,
∴四边形MENF是平行四边形.
点评 本题考查了平行四边形的性质与判定,关键是掌握平行四边形对角线互相平分;对角线互相平分的四边形是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
3.在解方程$\frac{x-1}{2}$-1=$\frac{3x+1}{3}$时,两边同时乘以6,去分母后,正确的是( )
| A. | 3x-1-6=2(3x+1) | B. | (x-1)-1=2(x+1) | C. | 3(x-1)-1=2(3x+1) | D. | 3(x-1)-6=2(3x+1) |
7.2017年某市将有5万名学生参加中考,为了解这些考生的数学成绩,中考后将从中抽取2000名考生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
| A. | 2000名考生是总体的一个样本 | |
| B. | 每个考生是个体 | |
| C. | 这5万名考生的数学中考成绩的全体是总体 | |
| D. | 统计中采用的调查方式是普查 |
4.六多边形的内角和为( )
| A. | 180° | B. | 360° | C. | 720° | D. | 1080° |
2.若关于x的方程x2-4x+c=0不存在实数根,则c的取值范围是( )
| A. | c>4 | B. | c≥4 | C. | c≤4 | D. | c<4 |
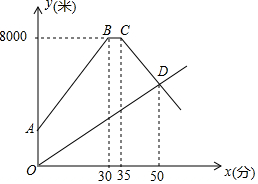 甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: