��Ŀ����
17����ͼ��������A��B��C�����Ӧ�����ֱ���a��b��14������a=2k-2����kΪ���ĸ�������BC=6������P��A���������������ÿ��1����λ�������������˶�������Q��C���������������ÿ��2����λ�������������˶���������ͬʱ�������˶�ʱ��Ϊt����1��a=-4��b=8��
��2����P��Q�����ľ���Ϊ14ʱ����t��ֵ��
��3������Q�ϵ�P��������ͷ����ͷʱ����Բ��ƣ�����ԭ�����ٶ����������˶�ֱ���ص�C�㣬��P�͵�Qͬʱֹͣ�˶�������P��Q����B�ľ���֮��Ϊ36ʱ����t��ֵ����ֱ��д����ʱP������ʾ������

���� ��1����kΪ��С�ĸ������������aֵ����BC=6��������ϵ�B��C֮��λ�ù�ϵ���������b��ֵ��
��2���ҳ��˶�ʱ��Ϊtʱ����P��Q��ʾ�������������ľ��빫ʽ���PQ=14�����ɵó�����t�ĺ�����ֵ����һԪһ�η��̣���֮���ɵó����ۣ�
��3����-4-t=14-2t�����Q�ϵ�P��ʱ�䣬��0��t��18��t��18��������ҳ���Q��ʾ�������ٸ���PB+QB=36�����ɵó�����t�ĺ�����ֵ����һԪһ�η��̣���֮���ɵó�tֵ����������P��ʾ�����м��ɣ�
��� �⣺��1����a=2k-2����kΪ���ĸ�������BC=6��
��k=-1��a=2����-1��-2=-4��b=14-6=8��
�ʴ�Ϊ��-4��8��
��2�����˶�ʱ��Ϊtʱ����P��Ӧ����Ϊ-4-t����Q��Ӧ����Ϊ14-2t��
��������ã�|14-2t-��-4-t��|=14��
��ã�t1=4��t2=32��
�൱P��Q�����ľ���Ϊ14ʱ��tΪ4���32�룮
��3����-4-t=14-2t��
��ã�t=18��
��-4-t=-22��
��0��t��18ʱ����Q��Ӧ����Ϊ14-2t����t��18ʱ����Q��Ӧ����Ϊ2t-22��
��0��t��18ʱ����PB+QB=36��
��[8-��-4-t��]+|8-��14-2t��|=36��
��ã�t=10��t=-18����ȥ����
��-4-t=-14��
��t��18ʱ����PB+QB=36��
��[8-��-4-t��]+|8-��2t-22��|=36��
��ã�t=18��t=6����ȥ����
��-4-t=-22��
��������������P��Q����B�ľ���֮��Ϊ36ʱ��tΪ10���18�룬��ʱP������ʾ����Ϊ-14��-22��
���� ���⿼��һԪһ�η��̵�Ӧ���Լ����ᣬ����Ĺؼ��ǣ���1��������ᣬ���a��bֵ����2������PQ=14���г�����t�ĺ�����ֵ����һԪһ�η��̣���3����0��t��18��t��18����������ǣ�

 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д� ����5��2���ϵ�д�
����5��2���ϵ�д�| A�� | k=3 | B�� | k��-3 | C�� | k��3 | D�� | -3��k��3 |
| A�� | $\frac{22}{7}$ | B�� | tan30�� | C�� | 3.14 | D�� | 2-1 |
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
| A�� |  | B�� |  | C�� |  | D�� |  |

| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
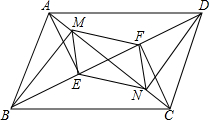 ��ͼ����֪?ABCD�ĶԽ���AC��BD����O��AE��BD��CF��BD��BM��AC��DN��AC��E��F��M��N�Ǵ��㣬����EN��NF��FM��ME����֤���ı���MENF��ƽ���ı��Σ�
��ͼ����֪?ABCD�ĶԽ���AC��BD����O��AE��BD��CF��BD��BM��AC��DN��AC��E��F��M��N�Ǵ��㣬����EN��NF��FM��ME����֤���ı���MENF��ƽ���ı��Σ�