��Ŀ����
 ��ͼ����ֱ֪��y=-3x+3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c������A�͵�C���Գ���Ϊֱ��l��x=-1������������x�����һ������ΪB��
��ͼ����ֱ֪��y=-3x+3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c������A�͵�C���Գ���Ϊֱ��l��x=-1������������x�����һ������ΪB����1����������ߵĽ���ʽ��
��2����P��ֱ��l�ϣ����ʹ��PAC���ܳ���С�ĵ�P�����ꣻ
��3����M�ڴ��������ϣ���N��y���ϣ���A��B��M��NΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ�ֱ��д����������Ҫ��ĵ�M�����ꣻ�����ܣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺���������ۺ���,ѹ����
��������1�����������ߵĽ���ʽ����������ߵĽ���ʽ��
��2��ֱ��BC��Գ���ֱ��l��x=-1�Ľ��㼴Ϊ����ʹ��PAC���ܳ���С�ĵ�P�����ꣻ
��3�����ۣ�����ABΪ�Խ��ߣ�����NA=MB���ı���ANBMΪƽ���ı��Σ����ȷ��M�ĺ����꣬Ȼ����������߽���ʽ�õ�M��������ꣻ����ABΪ��ʱ������ƽ���ı��ε����ʵõ�MN=AB=4�����ȷ��M�ĺ����꣬Ȼ����������߽���ʽ�õ�M��������꣮
��2��ֱ��BC��Գ���ֱ��l��x=-1�Ľ��㼴Ϊ����ʹ��PAC���ܳ���С�ĵ�P�����ꣻ
��3�����ۣ�����ABΪ�Խ��ߣ�����NA=MB���ı���ANBMΪƽ���ı��Σ����ȷ��M�ĺ����꣬Ȼ����������߽���ʽ�õ�M��������ꣻ����ABΪ��ʱ������ƽ���ı��ε����ʵõ�MN=AB=4�����ȷ��M�ĺ����꣬Ȼ����������߽���ʽ�õ�M��������꣮
����⣺��1��ֱ��y=-3x+3��x�ύ�ڵ�A����y�ύ�ڵ�C��
��y=0ʱ��-3x+3=0�����x=1��
��A��������1��0����
��x=0ʱ��y=3��
 ��C��������0��3����
��C��������0��3����
�����ߵĶԳ���Ϊֱ��x=-1��
��B��������-3��0����
��C��0��3������y=a��x-1����x+3����3=-3a��
���a=-1��
��������ߵĽ���ʽΪy=-��x-1����x+3��=-x2-2x+3��
��2����A����ֱ��l�ĶԳƵ��ǵ�B��-3��0��
��ͼ1������BC�����Գ����ڵ�P�����ʱ��PAC�ܳ���С��
��ֱ��BC�Ĺ�ϵʽΪ��y=mx+n��
��B��-3��0����C��0��3������y=mx+n��
��
���
��
��ֱ��bC�Ĺ�ϵʽΪy=x+3��
��x=-1ʱ��y=-1+3=2��
��P��������-1��2����
��3���ٵ���ABΪ�Խ��ߣ���ͼ2��
���ı���AMBNΪƽ���ı��Σ�
A�������Ϊ1��N�������Ϊ0��B�������Ϊ-3��
��M�������Ϊ-2��
��M��������Ϊy=-4+4+3=3��
��M��������-2��3����

�ڵ���ABΪ��ʱ����ͼ3��
���ı���ABMNΪƽ���ı��Σ�
��MN=AB=4����M1N1=4��M2N2=4��
��M1�ĺ�����Ϊ-4��M2�ĺ�����Ϊ4��
����y=-x2-2x+3��
��x=-4ʱ��y=-16+8+3=-5��
��x=4ʱ��y=-16-8+3=-21��
��M��������-4��-5����4��-21����
����������M��������-2��3����-4��-5����4��-21����
��y=0ʱ��-3x+3=0�����x=1��
��A��������1��0����
��x=0ʱ��y=3��
 ��C��������0��3����
��C������Ϊ��0��3���������ߵĶԳ���Ϊֱ��x=-1��
��B��������-3��0����
��C��0��3������y=a��x-1����x+3����3=-3a��
���a=-1��
��������ߵĽ���ʽΪy=-��x-1����x+3��=-x2-2x+3��
��2����A����ֱ��l�ĶԳƵ��ǵ�B��-3��0��
��ͼ1������BC�����Գ����ڵ�P�����ʱ��PAC�ܳ���С��
��ֱ��BC�Ĺ�ϵʽΪ��y=mx+n��
��B��-3��0����C��0��3������y=mx+n��
|
���
|
��ֱ��bC�Ĺ�ϵʽΪy=x+3��

��x=-1ʱ��y=-1+3=2��
��P��������-1��2����
��3���ٵ���ABΪ�Խ��ߣ���ͼ2��
���ı���AMBNΪƽ���ı��Σ�
A�������Ϊ1��N�������Ϊ0��B�������Ϊ-3��
��M�������Ϊ-2��
��M��������Ϊy=-4+4+3=3��
��M��������-2��3����

�ڵ���ABΪ��ʱ����ͼ3��
���ı���ABMNΪƽ���ı��Σ�
��MN=AB=4����M1N1=4��M2N2=4��
��M1�ĺ�����Ϊ-4��M2�ĺ�����Ϊ4��
����y=-x2-2x+3��
��x=-4ʱ��y=-16+8+3=-5��
��x=4ʱ��y=-16-8+3=-21��
��M��������-4��-5����4��-21����
����������M��������-2��3����-4��-5����4��-21����
���������⿼���˶��κ����ۺ��⣺���κ���y=ax2+bx+c��a��b��cΪ������a��0����ͼ��Ϊ�����ߣ��䶥��ʽΪy=a��x-
��2+
�������ߵĶԳ���Ϊx=-
����a��0��y��Сֵ=
����a��0��y���ֵ=
���������ϵĵ�ĺ����������������ߵĽ���ʽ�����������ı��ε��ж�������Ҫ�������ã�
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 4ac-b2 |
| 4a |

��ϰ��ϵ�д�
 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
�����Ŀ
���л�����ȷ���ǣ�������
| A��-[-��-10��]=-10 |
| B��-��-3��=-3 |
| C��-��+5��=5 |
| D��-[-��+8��]=-8 |
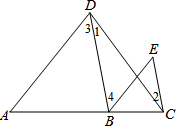 ��ͼ��գ���ע�����ɣ�
��ͼ��գ���ע�����ɣ�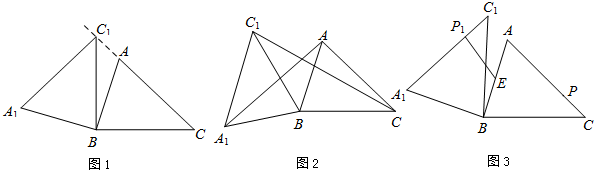
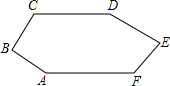 ��ͼ����֪CD��AF����CDE=��BAF��AB��BC����C=124�㣬��E=80�㣬���F�Ĵ�С��
��ͼ����֪CD��AF����CDE=��BAF��AB��BC����C=124�㣬��E=80�㣬���F�Ĵ�С�� ��ͼ��һ�κ���y=ax+b��ͼ���뷴��������y=
��ͼ��һ�κ���y=ax+b��ͼ���뷴��������y=