题目内容
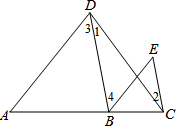 按图填空,并注明理由.
按图填空,并注明理由.已知:如图,∠1=∠2,∠3=∠E.
求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴
(
∴∠E=∠
(
又∵∠E=∠3 ( 已知 )
∴∠3=∠
(
∴AD∥BE.
(
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定定理和平行线的性质进行填空.
解答:证明:∵∠1=∠2 (已知)
∴EC∥DB
( (内错角相等,两直线平行 )
∴∠E=∠4
( 两直线平行,内错角相等 )
又∵∠E=∠3 ( 已知 )
∴∠3=∠4
( 等量代换 )
∴AD∥BE.
( 内错角相等,两直线平行 ).
故答案是:BD;CE;(内错角相等,两直线平行);4;(两直线平行,内错角相等);4(等量代换);(内错角相等,两直线平行).
∴EC∥DB
( (内错角相等,两直线平行 )
∴∠E=∠4
( 两直线平行,内错角相等 )
又∵∠E=∠3 ( 已知 )
∴∠3=∠4
( 等量代换 )
∴AD∥BE.
( 内错角相等,两直线平行 ).
故答案是:BD;CE;(内错角相等,两直线平行);4;(两直线平行,内错角相等);4(等量代换);(内错角相等,两直线平行).
点评:本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
下列式子:①
;②
;③
;④
.其中是二次根式的有( )
|
| -5 |
| 3 | 8 |
| (-2)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
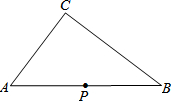 如图,P是Rt△ABC斜边AB上一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )
如图,P是Rt△ABC斜边AB上一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )| A、1条 | B、2条 | C、3条 | D、4条 |
如果把分式
中的a、b都扩大5倍,那么分式的值一定( )
| 5ab |
| a-2b |
| A、扩大5倍 | B、扩大25倍 |
| C、不变 | D、缩小5倍 |
下列计算中正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
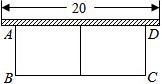 如图,有长为30m的篱笆,一面得用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.
如图,有长为30m的篱笆,一面得用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.
 如图,已知直线y=-3x+3与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过点A和点C,对称轴为直线l:x=-1,该抛物线与x轴的另一个交点为B.
如图,已知直线y=-3x+3与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过点A和点C,对称轴为直线l:x=-1,该抛物线与x轴的另一个交点为B.