��Ŀ����
����ǡ�ABC�У���ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1��
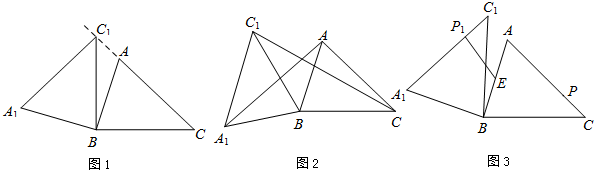
��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1B���CC1A1�Ķ�����
��2����ͼ2������BAC=75�㣬BC=6������AA1��CC1������ת�����У���ת�Ǧ���0�㣼����360�㣩Ϊ���ٶ���ʱAA1��BC1���������ʱ��CBC1�������
��3����ͼ3����AB=5��BC=6����EΪ�߶�AB�е㣬��P���߶�AC�ϵ�����һ�㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ���Сֵ��

��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1B���CC1A1�Ķ�����
��2����ͼ2������BAC=75�㣬BC=6������AA1��CC1������ת�����У���ת�Ǧ���0�㣼����360�㣩Ϊ���ٶ���ʱAA1��BC1���������ʱ��CBC1�������
��3����ͼ3����AB=5��BC=6����EΪ�߶�AB�е㣬��P���߶�AC�ϵ�����һ�㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ���Сֵ��
���㣺��ת������
ר�⣺
��������1��������ת�����ʿɵã���A1C1B=��ACB=45�㣬BC=BC1�����ɵ��������ε����ʣ�������á�CC1A1�Ķ�����
��2���ɡ�ABC�ա�A1BC1����֤�á�ABA1�ס�CBC1��Ȼ���������������ε�����ȵ������Ʊȵ�ƽ����������á�CBC1�������
��3���ɵ�P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����������߶�EP1���ȵ���Сֵ��
��2���ɡ�ABC�ա�A1BC1����֤�á�ABA1�ס�CBC1��Ȼ���������������ε�����ȵ������Ʊȵ�ƽ����������á�CBC1�������
��3���ɵ�P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����������߶�EP1���ȵ���Сֵ��
����⣺��1������ת�����ʿɵã���A1C1B=��ACB=45�㣬BC=BC1��
���CC1B=��C1CB=45�㣬
���CC1A1=��CC1B+��A1C1B=45��+45��=90�㣮
��2���ߡ�ABC�ա�A1BC1��
��BA=BA1��BC=BC1����ABC=��A1BC1��
��
=
����ABC+��ABC1=��A1BC1+��ABC1��
���ABA1=��CBC1��
���ABA1�ס�CBC1��
��
=��
��2
������BAC=75�㣬BC=6��
��AB=6
-6��
��S��ABA1=
��6����3
-3��=9
-9��
��S��CBC1=��4-2
������9
-9��=54
-90��
��3����ͼ1��
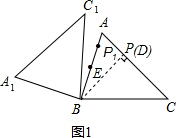
����B��BD��AC��DΪ���㣬
�ߡ�ABCΪ��������Σ�
���D���߶�AC�ϣ�
��Rt��BCD��BD=BC��sin45��=3
��
��P��AC���˶���BP��AC��ֱ��ʱ��ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����СֵΪ��EP1=BP1-BE=BD-BE=3
-
��
���CC1B=��C1CB=45�㣬
���CC1A1=��CC1B+��A1C1B=45��+45��=90�㣮
��2���ߡ�ABC�ա�A1BC1��
��BA=BA1��BC=BC1����ABC=��A1BC1��
��
| BA |
| BC |
| BA1 |
| BC1 |
���ABA1=��CBC1��
���ABA1�ס�CBC1��
��
| S��ABA1 |
| S��CBC1 |
| BA |
| BC |
������BAC=75�㣬BC=6��
��AB=6
| 3 |
��S��ABA1=
| 1 |
| 2 |
| 3 |
| 3 |
��S��CBC1=��4-2
| 3 |
| 3 |
| 3 |
��3����ͼ1��

����B��BD��AC��DΪ���㣬
�ߡ�ABCΪ��������Σ�
���D���߶�AC�ϣ�
��Rt��BCD��BD=BC��sin45��=3
| 2 |
��P��AC���˶���BP��AC��ֱ��ʱ��ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����СֵΪ��EP1=BP1-BE=BD-BE=3
| 2 |
| 5 |
| 2 |
���������⿼������ת�����ʡ����������ε��ж������ʡ�ȫ�������ε��ж��������Լ����Ǻ�����Ӧ�ã�ע�����ν��˼���Ӧ�ã�ע����תǰ��Ķ�Ӧ��ϵ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��a-b=2��a-c=1����2a-b-c��2+��c-b��2��ֵΪ��������
| A��10 | B��11 | C��9 | D��12 |
����ѷ�ʽ
�е�a��b������5������ô��ʽ��ֵһ����������
| 5ab |
| a-2b |
| A������5�� | B������25�� |
| C������ | D����С5�� |
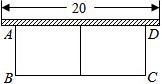 ��ͼ���г�Ϊ30m����ʣ�һ�����ǽ��ǽ�������ó���Ϊ20m����Χ���м����һ����ʣ�ƽ����AB���ľ��λ��ԣ�
��ͼ���г�Ϊ30m����ʣ�һ�����ǽ��ǽ�������ó���Ϊ20m����Χ���м����һ����ʣ�ƽ����AB���ľ��λ��ԣ�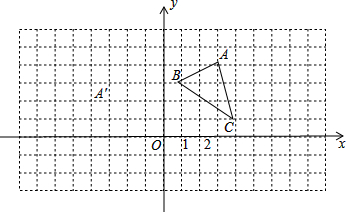
 ��ͼ����ֱ֪��y=-3x+3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c������A�͵�C���Գ���Ϊֱ��l��x=-1������������x�����һ������ΪB��
��ͼ����ֱ֪��y=-3x+3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c������A�͵�C���Գ���Ϊֱ��l��x=-1������������x�����һ������ΪB��