题目内容
求证:对任何矩形A,总存在一个矩形B,使得矩形B与矩形A的周长和面积比等于同一个常数k(k≥1).
考点:根的判别式
专题:证明题
分析:设已知矩形A的长与宽分别为a,b,所求矩形B的长与宽为x,y,则矩形A的周长是2(a+b),面积为ab,矩形B的周长为2(x+y),面积为xy,得出方程组,转化成方程后求出△的值,即可得出答案.
解答:解:设已知矩形A的长与宽分别为a,b,所求矩形B的长与宽为x,y,
则矩形A的周长是2(a+b),面积为ab,
矩形B的周长为2(x+y),面积为xy,
则
∴x,y是方程t2-k(a+b)t+kab=0的两实根.
当△=[k(a+b)]2-4kab≥0,即k≥
时,方程有解.
所以,对于长与宽分别为a,b的矩形,当k≥
时,存在周长与面积都是已知矩形的k倍的矩形.
∵(a-b)2≥0,
∴a2+b2≥2ab,a2+b2+2ab≥4ab,
即(a+b)2≥4ab,
≤1,
∴
的最大值为1.
∴当k≥1时,所有的矩形都有周长与面积同时扩大m倍的矩形,
即对任何矩形A,总存在一个矩形B,使得矩形B与矩形A的周长和面积比等于同一个常数k(k≥1).
则矩形A的周长是2(a+b),面积为ab,
矩形B的周长为2(x+y),面积为xy,
则
|
∴x,y是方程t2-k(a+b)t+kab=0的两实根.
当△=[k(a+b)]2-4kab≥0,即k≥
| 4ab |
| (a+b)2 |
所以,对于长与宽分别为a,b的矩形,当k≥
| 4ab |
| (a+b)2 |
∵(a-b)2≥0,
∴a2+b2≥2ab,a2+b2+2ab≥4ab,
即(a+b)2≥4ab,
| 4ab |
| (a+b)2 |
∴
| 4ab |
| (a+b)2 |
∴当k≥1时,所有的矩形都有周长与面积同时扩大m倍的矩形,
即对任何矩形A,总存在一个矩形B,使得矩形B与矩形A的周长和面积比等于同一个常数k(k≥1).
点评:本题考查了一元二次方程根的判别式的应用,注意:一元二次方程ax2+bx+c=0,(a、b、c为常数,a≠0),当b2-4ac>0时,方程有两个不相等的实数根,当b2-4ac=0时,方程有两个相等的实数根,当b2-4ac<0时,方程无实数根,题目比较好,难度偏大.

练习册系列答案
相关题目
若α为锐角,则sinα+cosα的值( )
| A、总小于1 |
| B、总大于1 |
| C、总等于1 |
| D、可能大于1,也可能小于1或等于1 |
某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板,他购买的瓷砖形状不可以是( )
| A、正三角形 | B、长方形 |
| C、正八边形 | D、正六边形 |
下面四个图形中,∠l与∠2是对顶角的图形是( )
A、 |
B、 |
C、 |
D、 |
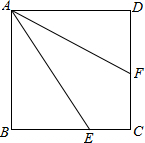 已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.
已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.