题目内容
6.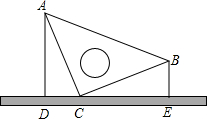 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )| A. | 6.5cm | B. | 5cm | C. | 9.5cm | D. | 11cm |
分析 只要证明△ADC≌△CEB,可得DC=BE=3cm,AD=CE,由DE=8cm,可得AD=CE=5cm.
解答 解: ∵∠ADC=∠BEC=∠ACB=90°,
∵∠ADC=∠BEC=∠ACB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠DAC=∠BCE}\\{∠ADC=∠BEC}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB,
∴DC=BE=3cm,AD=CE,
∵DE=8cm,
∴AD=CE=5cm.
故选B.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
16.数学考试成绩85分以上为优秀,以85分为标准,老师将某一小组五名同学的成绩记为-9、-4、+11、-7、0,这五名同学的实际成绩最高的应是( )
| A. | 93分 | B. | 85分 | C. | 96分 | D. | 78分 |
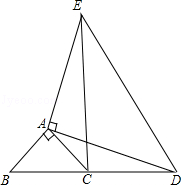 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.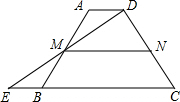 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.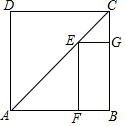 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.