题目内容
18.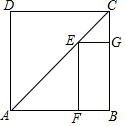 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.
分析 只要证明EF=AF,EG=BF即可解决问题.
解答 解 :∵E是正方形ABCD对角线AC上一点,
:∵E是正方形ABCD对角线AC上一点,
∴∠BAC=∠ACB=45°,∠B=90°
∵EF⊥AB,EG⊥BC,F、G是垂足,
∴∠B=∠EFB=∠EGB=90°,
∴四边形EFBG是矩形,
∴EG=BF,
∵△AEF是等腰直角三角形,
∴EF=AF,
∵正方形ABCD周长为a,
∴AB=$\frac{1}{4}$a,
∴EF+EG=AF+BF=AB=$\frac{1}{4}$a.
点评 本题主要考查正方形的性质、矩形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会用转化的思想思考问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
6.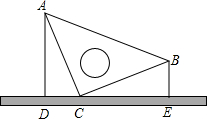 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )| A. | 6.5cm | B. | 5cm | C. | 9.5cm | D. | 11cm |
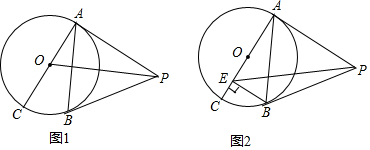 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径. 如图,斜折一页书的一角,使点A落在同一书页的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE等于多少度,并说明理由.
如图,斜折一页书的一角,使点A落在同一书页的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE等于多少度,并说明理由.