题目内容
17.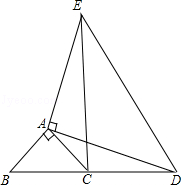 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.(1)求证:BD=CE.
(2)BD,CE有什么位置关系?请证明.
分析 (1)根据等腰三角形的性质可得出AB=AC、AD=AE,由∠BAC=∠DAE=90°可得出∠BAD=∠CAE,由此即可证出△BAD≌△CAE(SAS),根据全等三角形的性质即可得出BD=CE;
(2)根据等腰直角三角形的性质可得出∠ABC=∠ACB=45°,根据全等三角形的性质可得出∠ACE=∠ABC=45°,进而即可得出∠BCE=∠ACB+∠ACE=90°,即BD⊥CE.
解答 证明:(1)∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AD=AE.
∵∠BAC=90°,∠DAE=90°,
∴∠BAC+∠CAD=∠CAD+∠CAE,
即∠BAD=∠CAE.
在△BAD和△CAE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)BD⊥CE.
∵△ABC是等腰三角形,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵△BAD≌△CAE,
∴∠ACE=∠ABC=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∴BD⊥CE.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质以及等腰直角三角形,解题的关键是:(1)利用全等三角形的判定定理SAS证出△BAD≌△CAE;(2)根据等腰直角三角形的性质结合全等三角形的性质找出∠ACB=∠ACE=45°.

练习册系列答案
相关题目
5.已知当a=1,b=-2时,代数式ab+bc+ac=10,则c的值为( )
| A. | 12 | B. | 6 | C. | -12 | D. | -64 |
6.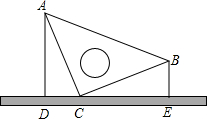 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )| A. | 6.5cm | B. | 5cm | C. | 9.5cm | D. | 11cm |
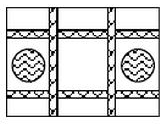 “G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.
“G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.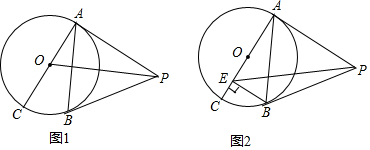 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.