题目内容
7.如图,C为圆周上一点,BD是☉O的切线,B为切点.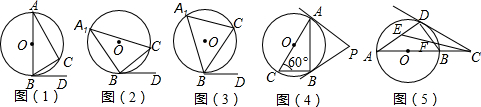
(1)在图(1)中,AB是☉O的直径,∠BAC=30°,则∠DBC的度数为30°.
(2)在图(2)中,∠BA1C=40°,求∠DBC的度数.
(3)在图(3)中,∠BA1C=α,求∠DBC的大小.
(4)通过(1)、(2)、(3)的探究,你发现的结论是弦切角等于它夹的弧所对的圆周角
(5)如图(4),AC是☉O的直径,∠ACB=60°,连接AB,过A、B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为3$\sqrt{3}$.
(6)如图(5),C是⊙O的直径AB延长线上的一点,CD切⊙O于D,∠ACD的平分线分别交AD、BD于E、F,试猜想∠DEF的度数并说明理由.
分析 (1)由切线的性质和圆周角定理以及角的互余关系得出∠DBC=∠A=30°即可;
(2)连接AC,由(1)得出∠DBC=∠A,由圆周角定理得出∠A=∠A1,即可得出∠DBC=∠BA1C=40°;
(3)由(2)得出∠DBC=∠BA2C=α即可;
(4)∠DBC等于$\widehat{BC}$所对的圆周角,得出弦切角定理;
(5)先在RtABC求出BC,再判断出三角形PAB是等边三角形即可求出结论;
(6)先判断出∠CAD=$\frac{1}{2}$∠COD,∠ACE=$\frac{1}{2}$∠ACD,再利用切线得出∠COD+∠ACD=90°,最后用三角形的外角的性质即可得出结论;
解答 解:(1)
∵BD是⊙0的切线,
∴∠ABO=90°,
即∠ABC+∠DBC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠A+∠ABC=90°,
∴∠DBC=∠A=30°;
故答案为:30°,
(2)连接BO交⊙O于A,连接AC,如图所示:
由(1)得:∠DBC=∠A,
又∵∠A=∠A1,
∴∠DBC=∠BA1C=40°;
(3)由(2)得:∠DBC=∠BA2C=α;
(4)∠DBC等于$\widehat{BC}$所对的圆周角;
弦切角等于它夹的弧所对的圆周角,
故答案为:弦切角等于它夹的弧所对的圆周角;
(5)连接如图OB,
在Rt△ABC中,AC=2OA=2,∠ACB=60°,
∴AB=$\sqrt{3}$,∠AOB=120°
∵PA,PB分别与⊙O相切,
∴∠PAO=∠PBO=90°,PA=PB
∴∠APB=60°,
∴△PAB是等边三角形,
∴PA=PB=AB=$\sqrt{3}$,
∴△PAB的周长为3$\sqrt{3}$,
故答案为3$\sqrt{3}$;
(6)如图5,
连接OD,
∴∠DAC=$\frac{1}{2}$∠COD,
∵CD是⊙O的切线,
∴∠ODC=90°,
∴∠ACD+∠COD=90°,
∵CE是∠ACD的角平分线,
∴∠ACE=$\frac{1}{2}$∠ACD
∴∠DEF=∠DAC+∠ACE=$\frac{1}{2}$∠COD+$\frac{1}{2}$∠ACD=$\frac{1}{2}$(∠COD+∠ACD)=45°.
点评 此题是圆的综合题,主要考查了圆的性质,三角形的内角和定理,圆周角的性质,切线的性质,三角形的外角的性质,解本题的关键是弦切角等于它夹的弧所对的圆周角的得出.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案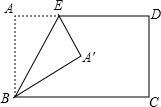 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | a=1,b=1 | B. | a=-1,b=1 | C. | a=-1,b=2 | D. | a=1,b=2 |
 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( )
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( )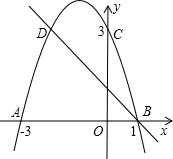 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.