题目内容
12.在直角坐标系中,已知A(1,5),B(4,-2),C(1,0)三点.(1)点A关于x轴的对称的A′的坐标为(1,-5);
点B关于y轴的对称点B′的坐标为(-4,-2);
点C关于y轴的对称点C′的坐标为(-1,0).
(2)求(1)中△A′B′C′的面积.
分析 (1)根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案;根据关于y轴对称的点的纵坐标相等,横坐标互为相反数,可得答案;
(2)根据三角形的面积公式,可得答案.
解答 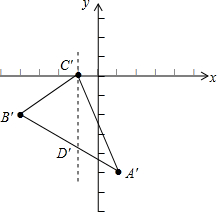 解:(1)点A关于x轴的对称的A′的坐标为 (1,-5);
解:(1)点A关于x轴的对称的A′的坐标为 (1,-5);
点B关于y轴的对称点B′的坐标为 (-4,-2);
点C关于y轴的对称点C′的坐标为 (-1,0);
故答案为:(1,-5);(-4,-2);(-1,0).
(2)作C′D′平行于y轴交B′A′于D′,如右图所示,
设过点A′B′的直线解析式为y=kx+b,
$\left\{\begin{array}{l}{k+b=-5}\\{-4k+b=-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-0.6}\\{b=-4.4}\end{array}\right.$,
即过点A′B′的直线解析式为y=-0.6x-4.4,
将x=-1代入y=-0.6x-4.4,得y=-3.8,
∴△A′B′C′的面积是:$\frac{3.8×[(-1)-(-4)]}{2}+\frac{3.8×[1-(-1)]}{2}$=9.5.
点评 本题考查关于x轴、y轴对称的点的坐标,解题的关键是明确题意,画出相应的图形,求出相应的图形的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各式中,是二次根式的是( )
| A. | π | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{-3}$ |
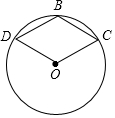 已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,
已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,
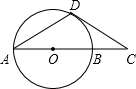 如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.