题目内容
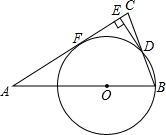 △ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E.
△ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E.(1)判断DE与⊙O的位置关系,并说明理由.
(2)若AC与⊙O相切于F,AB=5,sinA=
| 3 |
| 5 |
考点:切线的判定与性质
专题:
分析:(1)先连接OD,根据OB=OD,得出∠ABC=∠ODB,再根据AB=AC,得出∠ABC=∠ACB,∠ODB=∠ACB,从而证出OD∥AC,再根据DE⊥AC,即可得出DE与⊙O的位置关系;
(2)根据切线的性质定理,连接过切点的半径,运用锐角三角函数的定义,用半径表示OA的长,再根据AB的长列方程求解.
(2)根据切线的性质定理,连接过切点的半径,运用锐角三角函数的定义,用半径表示OA的长,再根据AB的长列方程求解.
解答: 解:(1)DE与⊙O相切;
解:(1)DE与⊙O相切;
理由如下:
连接OD,
∵OB=OD,
∴∠ABC=∠ODB;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC;
∵DE⊥AC,
∴OD⊥DE,
∴DE与⊙O相切.
(2)⊙O与AC相切于F点,连接OF,
则OF⊥AC,
在Rt△OAF中,sinA=
=
,
在Rt△OFA中,AO2=OF2+AF2,
∴OA=
OF,
又∵AB=OA+OB=5,
∴
OF+OF=5,
∴OF=
∴⊙O的半径
.
 解:(1)DE与⊙O相切;
解:(1)DE与⊙O相切;理由如下:
连接OD,
∵OB=OD,
∴∠ABC=∠ODB;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC;
∵DE⊥AC,
∴OD⊥DE,
∴DE与⊙O相切.
(2)⊙O与AC相切于F点,连接OF,
则OF⊥AC,
在Rt△OAF中,sinA=
| OF |
| AO |
| 3 |
| 5 |
在Rt△OFA中,AO2=OF2+AF2,
∴OA=
| 5 |
| 3 |
又∵AB=OA+OB=5,
∴
| 5 |
| 3 |
∴OF=
| 15 |
| 8 |
∴⊙O的半径
| 15 |
| 8 |
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可,解题时要熟练运用锐角三角函数的定义表示出两条边之间的关系.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠AOC=116°,则∠D的读数为( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠AOC=116°,则∠D的读数为( )| A、64° | B、58° |
| C、32° | D、29° |
两圆的直径分别为4和6,圆心距为10,则两圆的位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
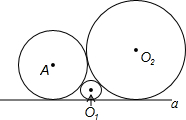 如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为
如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为 如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为
如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为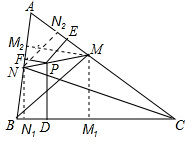 为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.