题目内容
[x]表示不超过x的最大整数部分,如[
]=3,[-3.14]=-4.解方程:[2x-1]=3x+
.
| 15 |
| 4 |
| 1 |
| 2 |
考点:取整计算
专题:
分析:首先令[2x-1]=n,代入原方程可得3x+
=n,即可求得x的值,又由[2x-1]≤2x-1<[2x-1]+1,可得n≤2•
-1<n+1,解此不等式组,即可求得n的值,继而可得x的值.
| 1 |
| 2 |
| 2n-1 |
| 6 |
解答:解:令[2x-1]=n,
代入原方程得:3x+
=n,
即:x=
,
又∵[2x-1]≤2x-1<[2x-1]+1,
∴n≤2•
-1<n+1,
整理得:3n≤2n-4<3n+3,解得:n=-4或-5或-6.
当n=-4时,原方程为:-4=3x+
,解得:x=-
;
当n=-5时,原方程为:-5=3x+
,解得:x=-
;
当n=-6时,原方程为:-6=3x+
,解得:x=-
.
经检验,得:x=-
,x=-
,x=-
均为原方程的解.
代入原方程得:3x+
| 1 |
| 2 |
即:x=
| 2n-1 |
| 6 |
又∵[2x-1]≤2x-1<[2x-1]+1,
∴n≤2•
| 2n-1 |
| 6 |
整理得:3n≤2n-4<3n+3,解得:n=-4或-5或-6.
当n=-4时,原方程为:-4=3x+
| 1 |
| 2 |
| 3 |
| 2 |
当n=-5时,原方程为:-5=3x+
| 1 |
| 2 |
| 11 |
| 6 |
当n=-6时,原方程为:-6=3x+
| 1 |
| 2 |
| 13 |
| 6 |
经检验,得:x=-
| 3 |
| 2 |
| 11 |
| 6 |
| 13 |
| 6 |
点评:此题考查了取整函数的知识.此题难度较大,解题的关键是掌握令[2x-1]=n,然后代入原方程求得x,由[2x-1]≤2x-1<[2x-1]+1,可得不等式组n≤2•
-1<n+1,注意取整函数的定义.
| 2n-1 |
| 6 |

练习册系列答案
相关题目
已知函数y=(a-2)x-3a-1,当自变量x的取值范围是3≤x≤5时,y既能达到大于5的值,又能取到小于3的值,则实数a的取值范围是( )
| A、a<3 | B、a>5 |
| C、a>8 | D、任意实数 |
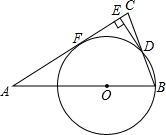 △ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E.
△ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E.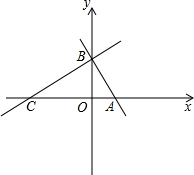 如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-
如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB- 如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=30°,则∠D的度数为
如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=30°,则∠D的度数为 如图是反比例函数
如图是反比例函数 这个直方图回答下面的问题:
这个直方图回答下面的问题: 如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是
如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是