题目内容
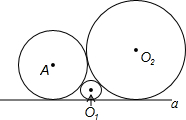 如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为
如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为考点:相切两圆的性质
专题:
分析:设直线a和圆A,圆O2相切于B,C两点,连接AB,O2C,过A作AH⊥O2C,过O1作O1E⊥AB于E,并反向延长O1E交O2C于F,根据相切两圆的性质:如果两圆相切,那么连心线必经过切点、切线的性质和勾股定理即可求出y与x的函数关系式.
解答: 解:设直线a和圆A,圆O2相切于B,C两点,连接AB,O2C,过A作AH⊥O2C,过O1作O1E⊥AB于E,并反向延长O1E交O2C于F,
解:设直线a和圆A,圆O2相切于B,C两点,连接AB,O2C,过A作AH⊥O2C,过O1作O1E⊥AB于E,并反向延长O1E交O2C于F,
∵⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).
∴AE=1-x,AO1=1+x,
在Rt△AEO1中,EO1=
=2
,
同理可求得:FO1=2
,
∴AH=EO1+O1F=2
+2
,
∵在Rt△AHO2中,AO2=1+y,O2H=y-1,
∴AH=
=2
,
∴2
+2
=2
,
∴
(1-
)=
,
∴y=
=
.
故答案为:y=
.
 解:设直线a和圆A,圆O2相切于B,C两点,连接AB,O2C,过A作AH⊥O2C,过O1作O1E⊥AB于E,并反向延长O1E交O2C于F,
解:设直线a和圆A,圆O2相切于B,C两点,连接AB,O2C,过A作AH⊥O2C,过O1作O1E⊥AB于E,并反向延长O1E交O2C于F,∵⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).
∴AE=1-x,AO1=1+x,
在Rt△AEO1中,EO1=
| AO 1 2-AE |
| x |
同理可求得:FO1=2
| xy |
∴AH=EO1+O1F=2
| x |
| xy |
∵在Rt△AHO2中,AO2=1+y,O2H=y-1,
∴AH=
| AO 2 2-O 2H 2 |
| y |
∴2
| x |
| xy |
| y |
∴
| y |
| x |
| x |
∴y=
| x | ||
(1-
|
x(1+
| ||
| 1-x |
故答案为:y=
x(1+
| ||
| 1-x |
点评:本题考查了相切两圆的性质:如果两圆相切,那么连心线必经过切点和切线的性质以及勾股定理的运用,解题的关键是添加辅助线,构造直角三角形,利用勾股定理求出某些线段的长.

练习册系列答案
相关题目
一个圆作滚动运动(如图),它从位置A开始,在与它相同的其它六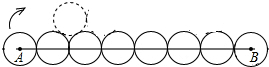 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.| A、3 | ||
B、
| ||
C、
| ||
D、
|
若不论k取什么实数,关于x的方程
-
=1(a、b是常数)的根总是x=1,则a+b=( )
| 2kx+a |
| 3 |
| x-bk |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
有一个六边形的半径为4cm,则这个六边形的面积为( )
A、6
| ||
B、12
| ||
C、24
| ||
D、48
|
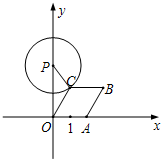 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t= 如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数
如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数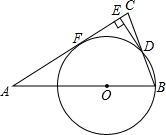 △ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E.
△ABC中,AB=AC,O在AB上,以O为圆心,OB为半径的圆与BC交于点D,DE⊥AC于E. 如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-
如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-