题目内容

如图，已知P为锐角△ABC内一点，过P分别作BC，AC，AB的垂线，垂足分别为D，E，F，BM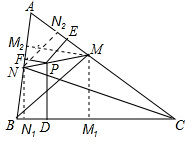为∠ABC的平分线，MP的延长线交AB于点N．如果PD=PE+PF，求证：CN是∠ACB的平分线．
考点：相似三角形的判定与性质,角平分线的性质,平行线分线段成比例
专题：证明题
分析：如图，作MM1⊥BC于点M1，MM2⊥AB于点M2，NN1⊥BC于点N1，NN2⊥AC于点N2．设NP=λNM，利用平行线分线段成比例证明N1D=λN1M1．作NH⊥MM1，分别交MM1，PD于点H，H1，可得△NPH1∽△NMH，利用相似三角形的性质可得：λMM1+（1-λ）NN1．同理可证明PD=λMM1+（1-λ）NN1．再由已知条件即可证明CN是∠ACB的平分线．
解答：证明：如图，作MM1⊥BC于点M1，MM2⊥AB于点M2，NN1⊥BC于点N1，NN2⊥AC于点N2．
设NP=λNM，
∵NN1∥PD∥MM1，
∴N1D=λN1M1．
若NN1＜MM1，如图，作NH⊥MM1，分别交MM1，PD于点H，H1，
则△NPH1∽△NMH，
∴
PH1
MH
=
NP
NM
=λ，
∴PH1=λMH，
∴PD=PH1+H1H=λMH+NN1=λ（MM1-NN1）+NN1=λMM1+（1-λ）NN1．
若NN1=MM1，则PD=NN1=MM1=λMM1+（1-λ）NN1．
若NN1＞MM1，
同理可证PD=λMM1+（1-λ）NN1．
∵PE∥NN2，∴
PE
NN2
=
PM
NM
=1-λ，
∴PE=（1-λ）NN2．
∵PF∥MM2，
∴
PF
MM2
=
NP
NM
=λ，
∴PF=λMM2．
又∵PD=PE+PF，
∴λMM1+（1-λ）NN1=λMM2+（1-λ）NN2．
又∵BM是∠ABC的平分线，
∴MM1=MM2，
∴（1-λ）NN1=（1-λ）NN2．
显然λ≠1，即1-λ≠0，
∴NN1=NN2，
∴CN是∠ACB的平分线．
点评：本题综合性的考查了平行线分线段成比例、相似三角形的判定和相似三角形的性质以及角平分线的判定方法，题目的难度很大，对学生的解题能力要求很高．
练习册系列答案
相关题目
如图，△OP1A1，△A1P2A2，△A2P3A3…都是等腰直角三角形，直角顶点P1，P2，P3…都在函数y=
4
x
（x＞0）的图象上，若三角形依次排列下去，则A2009的坐标是
 
．
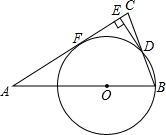△ABC中，AB=AC，O在AB上，以O为圆心，OB为半径的圆与BC交于点D，DE⊥AC于E．
（1）判断DE与⊙O的位置关系，并说明理由．
（2）若AC与⊙O相切于F，AB=5，sinA=
3
5
，求⊙O的半径．
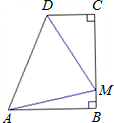如图，ABCD为直角梯形（∠B=∠C=90°），且AB=BC，若在边BC上存在一点M，使得△AMD为等边三角形，则
CD
AB
的值为
 
．
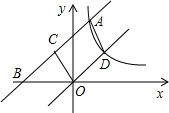如图，直线y=x+3交反比例函数y=
k
x
的图象于点A，交x轴于点B，且过点C（-1，2），将直线AB向下平移，线段CA平移到线段OD，当点D也在反比例函数y=
k
x
的图象上时，则k=
 
．
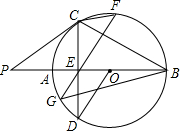已知：如图，AB是⊙O的直径，点P在BA的延长线上，弦CD交AB于E，连接OD、PC、BC，∠AOD=2∠ABC，∠P=∠D，过E作弦GF⊥BC交圆与G、F两点，连接CF、BG．则下列结论：
①CD⊥AB；②PC是⊙O的切线；③OD∥GF；④弦CF的弦心距等于
1
2
BG．则其中正确的是（　　）
A、①②④B、③④
C、①②③D、①②③④
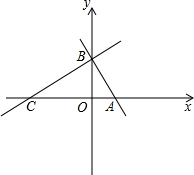如图，在平面直角坐标系中，点C（-3，0），点A、B分别在x轴、y轴的正半轴上，且满足（OB-
3
）2+
OA-1
=0．
（1）求点A、B的坐标；
（2）若点P从点C出发，以每秒1个单位的速度沿射线CB运动，连接AP．设△ABP的面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量t的取值范围．
（3）在（2）的条件下，是否存在点P，使以点A、B、P为顶点的三角形与△AOB相似？若存在，直接写出点P坐标；若不存在，说明理由．
如图，AB是⊙O的直径，点C、D在⊙O上，∠BAC=30°，则∠D的度数为
 
．
如图，在边长为1正方形ABCD中，E、F、G、H分别是AB、BC、CD、DA上的点，3AE=EB，有一只蚂蚁从E点出发，经过F、G、H，最后回点E点，则蚂蚁所走的最小路程是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网