题目内容
1．某玩具批发商销售进价为40元/只的玩具．市场调查发现，若以50元/只的价格出售，平均每天销售90只．售价每提高1元，平均每天就少销售3只．（1）要使平均每天的销售利润为1200元．应如何定价？
（2）物价部门规定每只售价不高于55元，则每只玩具的售价为多少元时，可获得最大利润？最大利润是多少元？
分析 （1）根据题意可以列出相应的方程，从而可以求得相应的售价；
（2）根据题意可以得到利润与售价之间的函数关系式，然后化为顶点式，即可解答本题．
解答 解：（1）要使平均每天的销售利润为1200元，设售价为x元/只，
（x-40）[90-（x-50）×3]=1200，
解得，x1=x2=60，
即要使平均每天的销售利润为1200元，售价为60元/只；
（2）设每只售价为x元，利润为W元，
W=（x-40）[90-（x-50）×3]=-3（x-60）2+1200，
∵x≤55，
∴当x=55时，W取得最大值，此时W=1125，
即每只玩具的售价为55元时，可获得最大利润，最大利润是1125元．
点评 本题考查二次函数的应用、一元二次方程的应用，解答此类问题的关键是明确题意，列出相应的函数解析式和方程，根据二次函数的顶点式和自变量的取值范围求出函数的最值．
练习册系列答案
相关题目
11．为了解石柱中学初2017届男生的身高，从中抽取了6名男生，测得身高（单位：cm）为：160，175，170，158，164，157，则这组数据的中位数和极差分别是（ ）
| A． | 161，18 | B． | 162，17 | C． | 162，18 | D． | 161，17 |
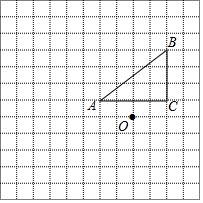如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A顺时针旋转90°，得到△AB′C′
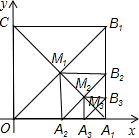如图，在平面直角坐标系中，边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1；以A1M1为对角线作第二个正方形A2A1B2M1，对角线A1M1和A2B2交于点M2；以A1M2为对角线作第三个正方形A3A1B3M2，对角线A1M2和A3B3交于点M3；…依此类推，这样作的第n个正方形对角线交点Mn的坐标是（$\frac{{2}^{n}-1}{{2}^{n}}$，$\frac{1}{{2}^{n}}$）．
11．已知：|x|=1，|y|=$\frac{1}{2}$，则（x20）3-x3y2的值等于（ ）
| A． | $-\frac{3}{4}$或$-\frac{5}{4}$ | B． | $\frac{3}{4}$或$\frac{5}{4}$ | C． | $\frac{3}{4}$ | D． | -$\frac{5}{4}$ |