题目内容
16.已知关于y的方程2y2+(m2-2m-15)y+m=0的两根互为相反数,则m的值为-3.分析 根据两根互为相反数,求出m的值,再由判别式判断方程是否有根,对使方程没有根的m的值要舍去.
解答 解:∵关于y的方程2y2+(m2-2m-15)y+m=0的两根互为相反数,
∴-$\frac{{m}^{2}-2m-15}{2}$=0,
∴m1=5,m2=-3.
∵当m=5时,原方程为:2y2+5=0,此时方程无解,
∴m=5不合题意舍去.
当m=-3时,原方程为:2y2-3=0,△>0,方程有解.
故答案是:-3.
点评 本题考查的是一元二次方程根与系数的关系,由两根互为相反数求出m的值,再由判别式把使方程没根的m的值舍去.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
5.下列代数式的书写格式正确的是( )
| A. | 1$\frac{1}{2}$abc | B. | n2 | C. | 3xy÷8 | D. | -$\frac{3}{4}$mn |
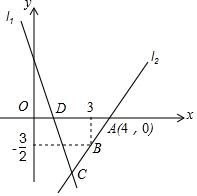 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C,在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标是(6,3).
如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C,在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标是(6,3).



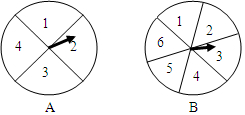 如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下: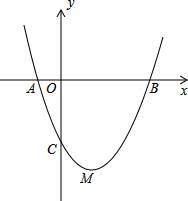 如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).
如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).