题目内容
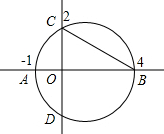 已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由.
已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由.考点:圆的综合题
专题:综合题
分析:连接CM,⊙M的半径为r,则CM=r,OM=r-1,在Rt△OCM根据勾股定理得22+(r-1)2=r2,解得r=
,则AB=2r=5,可得到B点坐标为(4,0),接着利用待定系数法求出直线BC的解析式为y=-
x+2,然后分类讨论:当PO=PB时,作BO的垂直平分线交直线BC于P,易得P点的横坐标为2,把x=2代入y=-
x+2得y=1,由此得到P点坐标为(2,1);当BP=BO=4时,设P点坐标为(t,-
t+2),利用两点间的距离公式得(t-4)2+(-
t+2)2=42,解得t1=
,t2=
,
则此时P点坐标为(
,-
)或(
,
);当OP=OB=4时,设P点坐标为(m,-
m+2),利用两点间的距离公式得m2+(-
m+2)2=42,
解得m1=-
,m2=4,则此时P点坐标为(-
,
).
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
20+8
| ||
| 5 |
20-8
| ||
| 5 |
则此时P点坐标为(
20+8
| ||
| 5 |
4
| ||
| 5 |
20-8
| ||
| 5 |
4
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m1=-
| 12 |
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
解答:解:存在.
连接CM,⊙M的半径为r,则CM=r,
∵A点坐标是(-1,0),C点坐标是(0,2),
∴OA=1,OC=2,
在Rt△OCM中,OM=r-1,
∵OC2+OM2=MC2,
 ∴22+(r-1)2=r2,解得r=
∴22+(r-1)2=r2,解得r=
,
∴AB=2r=5,
∴OB=4,
∴B点坐标为(4,0),
设直线BC的解析式为y=kx+b,
把B(4,0)、C(0,2)代入得
,解得
,
∴直线BC的解析式为y=-
x+2,
当PO=PB时,作BO的垂直平分线交直线BC于P,
∵OB=4,
∴P点的横坐标为2,
把x=2代入y=-
x+2得y=-1+2=1,
∴此时P点坐标为(2,1);
当BP=BO=4时,设P点坐标为(t,-
t+2),
∵PB=4,B(4,0)
∴(t-4)2+(-
t+2)2=42,
整理得5t2-40t+16=0,解得t1=
,t2=
,
∴此时P点坐标为(
,-
)或(
,
);
当OP=OB=4时,设P点坐标为(m,-
m+2),
∵OP=4,O(0,0)
∴m2+(-
m+2)2=42,
整理得5m2-48m-48=0,解得m1=-
,m2=4,
∴此时P点坐标为(-
,
),
综上所述,满足条件的P点坐标为(2,1)、(
,-
)、(
,
)、(-
,
).
连接CM,⊙M的半径为r,则CM=r,
∵A点坐标是(-1,0),C点坐标是(0,2),
∴OA=1,OC=2,
在Rt△OCM中,OM=r-1,
∵OC2+OM2=MC2,
 ∴22+(r-1)2=r2,解得r=
∴22+(r-1)2=r2,解得r=| 5 |
| 2 |
∴AB=2r=5,
∴OB=4,
∴B点坐标为(4,0),
设直线BC的解析式为y=kx+b,
把B(4,0)、C(0,2)代入得
|
|
∴直线BC的解析式为y=-
| 1 |
| 2 |
当PO=PB时,作BO的垂直平分线交直线BC于P,
∵OB=4,
∴P点的横坐标为2,
把x=2代入y=-
| 1 |
| 2 |
∴此时P点坐标为(2,1);
当BP=BO=4时,设P点坐标为(t,-
| 1 |
| 2 |
∵PB=4,B(4,0)
∴(t-4)2+(-
| 1 |
| 2 |
整理得5t2-40t+16=0,解得t1=
20+8
| ||
| 5 |
20-8
| ||
| 5 |
∴此时P点坐标为(
20+8
| ||
| 5 |
4
| ||
| 5 |
20-8
| ||
| 5 |
4
| ||
| 5 |
当OP=OB=4时,设P点坐标为(m,-
| 1 |
| 2 |
∵OP=4,O(0,0)
∴m2+(-
| 1 |
| 2 |
整理得5m2-48m-48=0,解得m1=-
| 12 |
| 5 |
∴此时P点坐标为(-
| 12 |
| 5 |
| 16 |
| 5 |
综上所述,满足条件的P点坐标为(2,1)、(
20+8
| ||
| 5 |
4
| ||
| 5 |
20-8
| ||
| 5 |
4
| ||
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
点评:本题考查了圆的综合题:理解与圆有关的性质和等腰三角形的判定;会运用勾股定理和两点间的距离公式计算线段的长;会解一元二次方程;学会运用分类讨论的思想解决数学问题.

练习册系列答案
相关题目
 如图,E为AB的中点,EP=EQ,∠AEP=∠BEQ.求证:DP=CQ.
如图,E为AB的中点,EP=EQ,∠AEP=∠BEQ.求证:DP=CQ. 一只蚂蚁从长为4cm、宽为3cm,高是5cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.
一只蚂蚁从长为4cm、宽为3cm,高是5cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.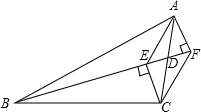 如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.
如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.