题目内容
已知关于x的一元二次方程x2-ax+a+5=0.
(1)无论a取任何值,该方程的根不可能为x=x0,写出x0的值,并证明.
(2)若a为正整数,且该方程存在正整数解,求所有正整数a的值.
(1)无论a取任何值,该方程的根不可能为x=x0,写出x0的值,并证明.
(2)若a为正整数,且该方程存在正整数解,求所有正整数a的值.
考点:一元二次方程的整数根与有理根,奇数与偶数,约数与倍数
专题:
分析:(1)当x=1时,无论a取任何值,等式的左边的值都是定值6,显然等式不成立.
(2)由条件可知根的判别式是完全平方数,故可设△=(a-2)2-24=t2(t为正整数),即(a-2+t)(a-2-t)=24.由a和t都是正整数可得a-2+t和a-2-t同奇同偶,都是非负整数,且a-2+t>a-2-t,故a-2+t和a-2-t分别为12、2或6、4,然后解方程组就可求出所有正整数a的值.
(2)由条件可知根的判别式是完全平方数,故可设△=(a-2)2-24=t2(t为正整数),即(a-2+t)(a-2-t)=24.由a和t都是正整数可得a-2+t和a-2-t同奇同偶,都是非负整数,且a-2+t>a-2-t,故a-2+t和a-2-t分别为12、2或6、4,然后解方程组就可求出所有正整数a的值.
解答:(1)答:x0=1.
证明:当x=1时,左边=1-a+a+5=6,右边=0,
∴左边≠右边.
∴该方程的根不可能为x=1.
(2)解:△=(-a)2-4×1×(a+5)=a2-4a-20=(a-2)2-24.
∵方程有正整数解,
∴可设△=(a-2)2-24=t2(t为正整数),
∴(a-2)2-t2=24.
∴(a-2+t)(a-2-t)=24.
∵a和t都是正整数,
∴a-2+t和a-2-t同奇同偶,都是非负整数,且a-2+t>a-2-t,
∴
或
.
解得:
或
.
∴满足条件的正整数a的值有9或7.
证明:当x=1时,左边=1-a+a+5=6,右边=0,
∴左边≠右边.
∴该方程的根不可能为x=1.
(2)解:△=(-a)2-4×1×(a+5)=a2-4a-20=(a-2)2-24.
∵方程有正整数解,
∴可设△=(a-2)2-24=t2(t为正整数),
∴(a-2)2-t2=24.
∴(a-2+t)(a-2-t)=24.
∵a和t都是正整数,
∴a-2+t和a-2-t同奇同偶,都是非负整数,且a-2+t>a-2-t,
∴
|
|
解得:
|
|
∴满足条件的正整数a的值有9或7.
点评:本题是一道竞赛题,涉及到奇数与偶数、约数、整系数的一元二次方程有正整数解、解二元一次方程组等知识,有一定的难度.需要说明的是:若整系数的一元二次方程有正整数解,则根的判别式必然是整数的平方;若m和n是整数,则m+n与m-n同奇同偶.

练习册系列答案
相关题目
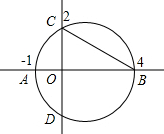 已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由.
已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由. 如图,直线y=k和双曲线y=
如图,直线y=k和双曲线y=