题目内容
 如图,E为AB的中点,EP=EQ,∠AEP=∠BEQ.求证:DP=CQ.
如图,E为AB的中点,EP=EQ,∠AEP=∠BEQ.求证:DP=CQ.考点:全等三角形的判定与性质
专题:证明题
分析:根据中点的性质,可得AE与BE的关系,根据SAS,可得△AEP与△BEQ的关系,根据全等三角形的性质,可得∠A与∠B的关系,根据ASA,可得△AED与△BEC的关系,根据全等三角形的性质,可得EC与ED的关系,根据等式的性质,可得答案.
解答:证明:∵E为AB的中点,
∴AE=BE.
在△AEP与△BEQ中,
,
∴△AEP≌△BEQ(SAS),
∴∠A=∠B,AP=BQ.
∵∠AEP=∠BEQ,
∴∠AEP+∠PED=∠BEQ+∠PED,
即∠AED=∠BEC.
在△AED与△BEC中,
,
∴△AED≌△BEC(ASA),
∴AD=BC.
∵AD-AP=BC-BQ,
∴DP=CQ.
∴AE=BE.
在△AEP与△BEQ中,
|
∴△AEP≌△BEQ(SAS),
∴∠A=∠B,AP=BQ.
∵∠AEP=∠BEQ,
∴∠AEP+∠PED=∠BEQ+∠PED,
即∠AED=∠BEC.
在△AED与△BEC中,
|
∴△AED≌△BEC(ASA),
∴AD=BC.
∵AD-AP=BC-BQ,
∴DP=CQ.
点评:本题考查了全等三角形的判定与性质,利用了SAS,ASA,证明三角形全等,利用了全等三角形的性质.

练习册系列答案
相关题目
用配方法解下列方程时,配方有误的是( )
| A、x2-2x-99=0化为(x-1)2=100 | ||||
B、2y2-7y-4=0化为(y-
| ||||
| C、x2-8x+4=0化为(x-2)2=0 | ||||
| D、x2+6x-5=0化为(x+3)2=14 |


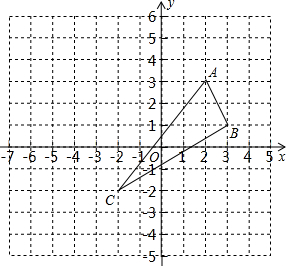 如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),
如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),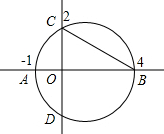 已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由.
已知如图,以AB为直径的圆交x轴于A、B两点,交y轴于C、D两点,其中圆心为点M,A点坐标是(-1,0),C点坐标是(0,2).请问在直线BC上是否存在一点P,使得以P、O、B三点构成的三角形是等腰三角形?若存在,求P点坐标;若不存在,请说明理由.