题目内容
14.先化简,再求值:$\frac{2a}{a+1}$-$\frac{2a-4}{{a}^{2}-1}$÷$\frac{a-2}{{a}^{2}-2a+1}$,其中x=-3是方程x2+2x+a=0的一个根.分析 先根据分式混合运算的法则把原式进行化简,把x=-3代入方程x2+2x+a=0求出a的值,再把a的值代入原式进行计算即可.
解答 解:原式=$\frac{2a}{a+1}$-$\frac{2(a-2)}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{a-2}$
=$\frac{2a}{a+1}$-$\frac{2(a-1)}{a+1}$
=$\frac{2}{a+1}$,
∵x=-3是方程x2+2x+a=0的一个根,
∴(-3)2+2×(-3)+a=0,解得a=-3,
当a=-3时,原式=-1.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的分式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出分式的值.

练习册系列答案
相关题目
5.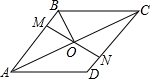 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
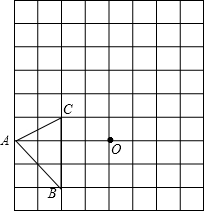 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算: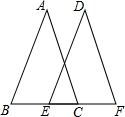 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )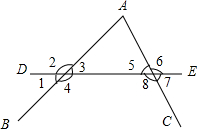 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角: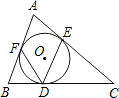 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.