ƒøƒ⁄»ð
»ÁÕº1£¨≈◊ŒÔœþy=nx2-11nx+24n£®n£º0£©”Îx÷·Ωª”⁄B°¢C¡Ωµ„£®µ„B‘⁄µ„Cµƒ◊Û≤ý£©£¨≈◊ŒÔœþ…œ¡Ì”–“ªµ„A‘⁄µ⁄“ªœÛœÞƒ⁄£¨«“°œBAC=90°„£Æ
£®1£©œþ∂ŒBCµƒ≥§Œ™ £ª
£®2£©¡¨Ω”OA£¨»Ù°˜OACŒ™µ»—¸»˝Ω«–Œ£¨«Ûn£ª
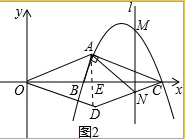
£®3£©»ÁÕº2£¨‘⁄£®2£©µƒÃıº˛œ¬£¨Ω´°˜OAC—ÿx÷·∑≠’€∫Ûµ√°˜ODC£¨µ„MŒ™µ„A”ε„C¡Ωµ„÷ƺ‰“ª∂ص„£¨«“µ„Mµƒ∫·◊¯±ÍŒ™m£¨π˝∂ص„M◊˜¥π÷±”⁄x÷·µƒ÷±œþl”ÎCDΩª”⁄µ„N£Æ ‘ÃΩæø£∫¢Ÿµ±MNπ˝ACµƒ÷–µ„ ±£¨≈–∂œÀƒ±þ–ŒAMCNµƒ–Œ◊¥£ª¢⁄µ±mŒ™∫Œ÷µ ±£¨Àƒ±þ–ŒAMCNµƒ√ʪ˝»°µ√◊Ó¥Û÷µ£¨≤¢«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£Æ

£®1£©œþ∂ŒBCµƒ≥§Œ™
£®2£©¡¨Ω”OA£¨»Ù°˜OACŒ™µ»—¸»˝Ω«–Œ£¨«Ûn£ª
£®3£©»ÁÕº2£¨‘⁄£®2£©µƒÃıº˛œ¬£¨Ω´°˜OAC—ÿx÷·∑≠’€∫Ûµ√°˜ODC£¨µ„MŒ™µ„A”ε„C¡Ωµ„÷ƺ‰“ª∂ص„£¨«“µ„Mµƒ∫·◊¯±ÍŒ™m£¨π˝∂ص„M◊˜¥π÷±”⁄x÷·µƒ÷±œþl”ÎCDΩª”⁄µ„N£Æ ‘ÃΩæø£∫¢Ÿµ±MNπ˝ACµƒ÷–µ„ ±£¨≈–∂œÀƒ±þ–ŒAMCNµƒ–Œ◊¥£ª¢⁄µ±mŒ™∫Œ÷µ ±£¨Àƒ±þ–ŒAMCNµƒ√ʪ˝»°µ√◊Ó¥Û÷µ£¨≤¢«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£Æ

øºµ„£∫∂˛¥Œ∫Ø ˝◊€∫œÃ‚
◊®Ã‚£∫
∑÷Œˆ£∫£®1£©∏˘æð∂˛¥Œ∫Ø ˝”Îx÷·Ωªµ„◊¯±Í«Û∑®£¨Ω‚“ª‘™∂˛¥Œ∑Ω≥ú¥ø…µ√≥ˆ£ª
£®2£©¿˚”√¡‚–Œ–‘÷ µ√≥ˆAD°ÕOC£¨Ω¯∂¯µ√≥ˆ°˜ACE°◊°˜BAE£¨º¥ø…µ√≥ˆAµ„◊¯±Í£¨Ω¯∂¯«Û≥ˆnµƒ÷µ£ª
£®3£©¢Ÿœ»«Û≥ˆMµƒ◊¯±Í£¨≈–∂œ «∑Ò‘⁄÷±œþOA…œ£¨»ª∫Û«Ûµ√÷±œþMC”Î÷±œþANµƒΩ‚Œˆ Ω≈–∂œÀ¸√«µƒ–±¬ «∑Òœýµ»£¨º¥ø…≈–∂œÀƒ±þ–Œµƒ–Œ◊¥£ª¢⁄ ◊œ»«Û≥ˆπ˝C°¢D¡Ωµ„µƒ◊¯±Íµƒ÷±œþCDµƒΩ‚Œˆ Ω£¨Ω¯∂¯¿˚”√SÀƒ±þ–ŒAMCN=S°˜AMN+S°˜CMN«Û≥ˆº¥ø…£Æ
£®2£©¿˚”√¡‚–Œ–‘÷ µ√≥ˆAD°ÕOC£¨Ω¯∂¯µ√≥ˆ°˜ACE°◊°˜BAE£¨º¥ø…µ√≥ˆAµ„◊¯±Í£¨Ω¯∂¯«Û≥ˆnµƒ÷µ£ª
£®3£©¢Ÿœ»«Û≥ˆMµƒ◊¯±Í£¨≈–∂œ «∑Ò‘⁄÷±œþOA…œ£¨»ª∫Û«Ûµ√÷±œþMC”Î÷±œþANµƒΩ‚Œˆ Ω≈–∂œÀ¸√«µƒ–±¬ «∑Òœýµ»£¨º¥ø…≈–∂œÀƒ±þ–Œµƒ–Œ◊¥£ª¢⁄ ◊œ»«Û≥ˆπ˝C°¢D¡Ωµ„µƒ◊¯±Íµƒ÷±œþCDµƒΩ‚Œˆ Ω£¨Ω¯∂¯¿˚”√SÀƒ±þ–ŒAMCN=S°˜AMN+S°˜CMN«Û≥ˆº¥ø…£Æ
Ω‚¥£∫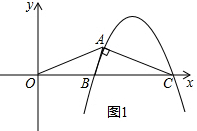 Ω‚£∫£®1£©°þ≈◊ŒÔœþy=nx2-11nx+24n £®n£º0£©”Îx÷·Ωª”⁄B°¢C¡Ωµ„£®µ„B‘⁄µ„Cµƒ◊Û≤ý£©£¨
Ω‚£∫£®1£©°þ≈◊ŒÔœþy=nx2-11nx+24n £®n£º0£©”Îx÷·Ωª”⁄B°¢C¡Ωµ„£®µ„B‘⁄µ„Cµƒ◊Û≤ý£©£¨
°ý≈◊ŒÔœþ”Îx÷·µƒΩªµ„◊¯±ÍŒ™£∫0=nx2-11nx+24n£¨
Ω‚µ√£∫x1=3£¨x2=8£¨
°ýOB=3£¨OC=8£¨
°ýBC=OC-OB=8-3=5£ª
£®2£©»ÁÕº2£¨◊˜AE°ÕOC£¨¥π◊„Œ™µ„E
°þ°˜OAC «µ»—¸»˝Ω«–Œ£¨
°ýOE=EC=
°¡8=4£¨
°ýBE=4-3=1£¨
”÷°þ°œBAC=90°„£¨
°ý°˜ACE°◊°˜BAE£¨
°ý
=
£¨
°ýAE2=BE•CE=1°¡4£¨
°ýAE=2£¨
°ýµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
∞—µ„Aµƒ◊¯±Í £®4£¨2£©¥˙»Î≈◊ŒÔœþy=nx2-11nx+24n£¨µ√n=-
£¨
£®3£©»ÁÕº2£¨¢Ÿ°þOB=3£¨OC=8£¨
°ýBµ„◊¯±ÍŒ™£®3£¨0£©£¨Cµ„◊¯±ÍŒ™£∫£®8£¨0£©£¨
°þn=-
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-
x2+
x-12£¨
°þÀƒ±þ–ŒAODC «¡‚–Œ£¨MN°Õx÷·£¨«“π˝ACµƒ÷–µ„£¨µ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
°ýNµ„µƒ◊¯±ÍŒ™£®6£¨-1£©£¨
∞—x=6¥˙»Îy=-
x2+
x-12£¨µ√£∫y=3£¨
°ýM£®6£¨3£©£¨
°þ÷±œþOAµƒΩ‚Œˆ ΩŒ™£∫y=
x£¨
°ýMµ„‘⁄÷±œþOA…œ£¨
°ýAM°ŒNC£¨
°þµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨Nµ„µƒ◊¯±ÍŒ™£®6£¨-1£©£¨
°ý÷±œþANµƒΩ‚Œˆ ΩŒ™£∫y=-
x+8£¨
°þC£®8£¨0£©£¨M£®6£¨3£©£¨
°ý÷±œþMCµƒΩ‚Œˆ ΩŒ™£∫y=-
x+12£¨
°ýAN°ŒMC£¨
°ýÀƒ±þ–ŒAMCN «∆Ω––Àƒ±þ–Œ£ª
¢⁄»ÁÕº2£¨°þµ„Mµƒ∫·◊¯±ÍŒ™m£¨«“µ„M‘⁄≈◊ŒÔœþy=-
x2+
x-12…œ£¨
°ýµ„Mµƒ◊¯±ÍŒ™ £®m£¨-
m2+
m-12£©£¨
°þµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
°ýµ„Dµƒ◊¯±ÍŒ™£®4£¨-2£©£¨
‘ÚC°¢D¡Ωµ„µƒ◊¯±Í«Û÷±œþCDµƒΩ‚Œˆ ΩŒ™y=
x-4£¨
°ýµ„Nµƒ◊¯±ÍŒ™ £®m£¨
m-4£©£¨
°ýMN=£®-
m2+
m-12£©-£®
m-4£©=-
m2+5m-8£¨
°ýSÀƒ±þ–ŒAMCN=S°˜AMN+S°˜CMN=
MN•CE=
£®-
m2+5m-8£©°¡4£¨
=-£®m-5£©2+9£¨
°ýµ±m=5 ±£¨Àƒ±þ–ŒAMCNµƒ√ʪ˝µƒ◊Ó¥Û÷µ=9£Æ
 Ω‚£∫£®1£©°þ≈◊ŒÔœþy=nx2-11nx+24n £®n£º0£©”Îx÷·Ωª”⁄B°¢C¡Ωµ„£®µ„B‘⁄µ„Cµƒ◊Û≤ý£©£¨
Ω‚£∫£®1£©°þ≈◊ŒÔœþy=nx2-11nx+24n £®n£º0£©”Îx÷·Ωª”⁄B°¢C¡Ωµ„£®µ„B‘⁄µ„Cµƒ◊Û≤ý£©£¨°ý≈◊ŒÔœþ”Îx÷·µƒΩªµ„◊¯±ÍŒ™£∫0=nx2-11nx+24n£¨
Ω‚µ√£∫x1=3£¨x2=8£¨
°ýOB=3£¨OC=8£¨
°ýBC=OC-OB=8-3=5£ª
£®2£©»ÁÕº2£¨◊˜AE°ÕOC£¨¥π◊„Œ™µ„E
°þ°˜OAC «µ»—¸»˝Ω«–Œ£¨
°ýOE=EC=
| 1 |
| 2 |
°ýBE=4-3=1£¨
”÷°þ°œBAC=90°„£¨
°ý°˜ACE°◊°˜BAE£¨
°ý
| AE |
| BE |
| CE |
| AE |
°ýAE2=BE•CE=1°¡4£¨
°ýAE=2£¨
°ýµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
∞—µ„Aµƒ◊¯±Í £®4£¨2£©¥˙»Î≈◊ŒÔœþy=nx2-11nx+24n£¨µ√n=-
| 1 |
| 2 |

£®3£©»ÁÕº2£¨¢Ÿ°þOB=3£¨OC=8£¨
°ýBµ„◊¯±ÍŒ™£®3£¨0£©£¨Cµ„◊¯±ÍŒ™£∫£®8£¨0£©£¨
°þn=-
| 1 |
| 2 |
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-
| 1 |
| 2 |
| 11 |
| 2 |
°þÀƒ±þ–ŒAODC «¡‚–Œ£¨MN°Õx÷·£¨«“π˝ACµƒ÷–µ„£¨µ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
°ýNµ„µƒ◊¯±ÍŒ™£®6£¨-1£©£¨
∞—x=6¥˙»Îy=-
| 1 |
| 2 |
| 11 |
| 2 |
°ýM£®6£¨3£©£¨
°þ÷±œþOAµƒΩ‚Œˆ ΩŒ™£∫y=
| 1 |
| 2 |
°ýMµ„‘⁄÷±œþOA…œ£¨
°ýAM°ŒNC£¨
°þµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨Nµ„µƒ◊¯±ÍŒ™£®6£¨-1£©£¨
°ý÷±œþANµƒΩ‚Œˆ ΩŒ™£∫y=-
| 3 |
| 2 |
°þC£®8£¨0£©£¨M£®6£¨3£©£¨
°ý÷±œþMCµƒΩ‚Œˆ ΩŒ™£∫y=-
| 3 |
| 2 |
°ýAN°ŒMC£¨
°ýÀƒ±þ–ŒAMCN «∆Ω––Àƒ±þ–Œ£ª
¢⁄»ÁÕº2£¨°þµ„Mµƒ∫·◊¯±ÍŒ™m£¨«“µ„M‘⁄≈◊ŒÔœþy=-
| 1 |
| 2 |
| 11 |
| 2 |
°ýµ„Mµƒ◊¯±ÍŒ™ £®m£¨-
| 1 |
| 2 |
| 11 |
| 2 |
°þµ„Aµƒ◊¯±ÍŒ™ £®4£¨2£©£¨
°ýµ„Dµƒ◊¯±ÍŒ™£®4£¨-2£©£¨
‘ÚC°¢D¡Ωµ„µƒ◊¯±Í«Û÷±œþCDµƒΩ‚Œˆ ΩŒ™y=
| 1 |
| 2 |
°ýµ„Nµƒ◊¯±ÍŒ™ £®m£¨
| 1 |
| 2 |
°ýMN=£®-
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
°ýSÀƒ±þ–ŒAMCN=S°˜AMN+S°˜CMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-£®m-5£©2+9£¨
°ýµ±m=5 ±£¨Àƒ±þ–ŒAMCNµƒ√ʪ˝µƒ◊Ó¥Û÷µ=9£Æ
µ„∆¿£∫±æÂøº≤È¡À∂˛¥Œ∫Ø ˝”Î◊¯±Í÷·µƒΩªµ„µƒ«Û∑®£¨∆Ω––Àƒ±þ–Œµƒ≈–∂®£¨¡‚–Œµƒ–‘÷ ∫ÕÀƒ±þ–Œ√ʪ˝µƒ«Û∑®µ»£Æ

¡∑œ∞≤·œµ¡–¥∞∏
œýπÿƒø
∂˛¥Œ∫Ø ˝y=x2-2x+2µƒÕºœÛ”Îx÷·µƒΩªµ„∏ˆ ˝ «£®°°°°£©
| A°¢0∏ˆ | B°¢1∏ˆ | C°¢2∏ˆ | D°¢3∏ˆ |
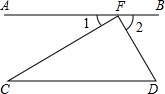 ÕÍ≥…œ¬√Ê÷§√˜£¨≤¢‘⁄œ¬√Ê¿®∫≈¿Ô£¨ÃÓ…œÕ∆¿Ìµƒ∏˘æð£Æ
ÕÍ≥…œ¬√Ê÷§√˜£¨≤¢‘⁄œ¬√Ê¿®∫≈¿Ô£¨ÃÓ…œÕ∆¿Ìµƒ∏˘æð£Æ »ÁÕº£¨Àƒ±þ–ŒABCDÀ˘‘⁄µƒÕ¯∏ÒÕº÷–£¨√ø∏ˆ–°’˝∑Ω–Œµƒ±þ≥§æ˘Œ™1∏ˆµ•Œª≥§∂»£Æ
»ÁÕº£¨Àƒ±þ–ŒABCDÀ˘‘⁄µƒÕ¯∏ÒÕº÷–£¨√ø∏ˆ–°’˝∑Ω–Œµƒ±þ≥§æ˘Œ™1∏ˆµ•Œª≥§∂»£Æ
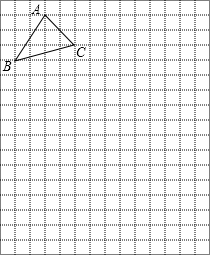 “—÷™£∫»ÁÕºµƒÕ¯∏Ò÷–£¨°˜ABCµƒ∂•µ„A£®0£¨5£©°¢B£®-2£¨2£©£Æ
“—÷™£∫»ÁÕºµƒÕ¯∏Ò÷–£¨°˜ABCµƒ∂•µ„A£®0£¨5£©°¢B£®-2£¨2£©£Æ