题目内容
二次函数y=x2-2x+2的图象与x轴的交点个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：抛物线与x轴的交点
专题：
分析：首先用△判定图象与x轴的交点情况；再判定与y轴交点的情况即可解答．
解答：解：因为△=b2-4ac=0=（-2）2-4×2=-4＜0，
所以该二次函数y=x2-2x+2的图象与x轴无交点．
故选：A．
所以该二次函数y=x2-2x+2的图象与x轴无交点．
故选：A．
点评：本题考查了抛物线与x轴的交点．二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系．
△=b2-4ac决定抛物线与x轴的交点个数．
△=b2-4ac＞0时，抛物线与x轴有2个交点；
△=b2-4ac=0时，抛物线与x轴有1个交点；
△=b2-4ac＜0时，抛物线与x轴没有交点．
△=b2-4ac决定抛物线与x轴的交点个数．
△=b2-4ac＞0时，抛物线与x轴有2个交点；
△=b2-4ac=0时，抛物线与x轴有1个交点；
△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
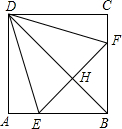如图，正方形ABCD中，点E，F分别在AB，BC边上，且△DEF是等边三角形，连接BD交EF于H，则∠FDH的度数为（ ）| A、15° | B、20° |
| C、25° | D、30° |
下列计算中正确的是（ ）
A、
| ||||||||||||||
B、（a-1）
| ||||||||||||||
C、
| ||||||||||||||
D、
|
直线y=x+3与x轴的交点是（ ）
| A、（-3，0） |
| B、（0，-3） |
| C、（0，3） |
| D、（3，0） |
用科学记数法表示0.000 000 501应记为（ ）
| A、5.01×10-8 |
| B、5.01×10-7 |
| C、5.01×107 |
| D、5.01×108 |
已知单项式-2x2y3与-5xayb是同类项，则a+b=（ ）
| A、5 | B、3 | C、4 | D、2 |
