Question

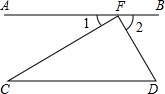完成下面证明，并在下面括号里，填上推理的根据．
如图，已知∠1和∠D互余，CF⊥DF，求证：AB∥CD．
证明：∵CF⊥DF（已知）
∴∠CFD=90°（

 

）
∴∠1+∠2=180°-∠CFD=90°（平角的定义）
∵∠1和∠D互余（已知）
∴∠1+∠D=

 

（余角的定义）
∴∠2=

 

（等量代换）
∴AB∥CD（

 

）

Answer 1

考点：平行线的判定,垂线

专题：推理填空题

分析：根据平行线的判定定理进行解答即可．

解答：证明：∵CF⊥DF（已知），
∴∠CFD=90°（垂直的定义），
∴∠1+∠2=180°-∠CFD=90°（平角的定义）．
∵∠1和∠D互余（已知），
∴∠1+∠D=90°（余角的定义），
∴∠2=∠D（等量代换），
∴AB∥CD（内错角相等，两直线平行）．
故答案为：垂直的定义，90°，∠D，内错角相等，两直线平行．

点评：本题考查的是平行线的判定定理，用到的知识点为：内错角相等，两直线平行．