题目内容
5．
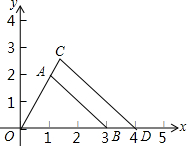如图，△AOB以O为位似中心，扩大到△COD，各点的坐标分别为A（1，2），B（3，0），D（4，0），求点C的坐标，并求出四边形ABDC的面积．
分析 根据题意计算出△AOB的面积，根据相似三角形的面积比等于相似比的平方计算出△COD的面积，计算即可．
解答 解：∵A（1，2），B（3，0），
∴S△AOB=$\frac{1}{2}$×3×2=3，
∵△OAB∽△OCD，$\frac{OB}{OD}$=$\frac{3}{4}$，
∴S△OAB：S△OCD=9：16，
∴S△OCD=$\frac{16}{3}$，
∴四边形ABDC的面积=$\frac{16}{3}$-3=$\frac{7}{3}$．
点评 本题考查的是位似变换的定义坐标与图形的性质以及相似三角形的性质，如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形、相似三角形的面积比等于相似比的平方．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
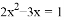的二次项系数、一次项系数、常数项分别是()
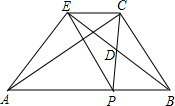如图，在Rt△ABC中，∠ACB=90°，点P是斜边AB上一个动点（不与A、B重合），连接PC，点D是PC的中点，连接BD并延长至E，使DE=BD，连接EA、EP、EC．
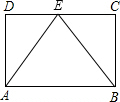如图，平行四边形ABCD中，E是CD的中点，△ABE是等边三角形．求证：四边形ABCD是矩形．