题目内容
16.有四张正面分别标有数字-2,0,1,2的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的函数y=(a+1)x2+ax+1的图象与x轴没有交点,且使关于x的不等式组$\left\{\begin{array}{l}{x+2≥a}\\{1-x≥2a}\end{array}\right.$有解的概率为$\frac{1}{2}$.分析 由y=(a+1)x2+ax+1的图象与x轴没有交点,依据根的判别式△=b2-4ac<0、联立二次项系数>0得出关于a的一元二次不等式组,解不等式组可得出a的取值范围;根据关于x的不等式组$\left\{\begin{array}{l}{x+2≥a}\\{1-x≥2a}\end{array}\right.$有解亦可得出a的取值范围;将两个条件合在一起结合题意,可知a只能为0或1,结合随机事件的概率公式即可得出结论.
解答 解:∵y=(a+1)x2+ax+1的图象与x轴没有交点,
∴$\left\{\begin{array}{l}{a+1>0}\\{{a}^{2}-4(a+1)<0}\end{array}\right.$,
解得:2-2$\sqrt{2}$<a<2+2$\sqrt{2}$.
解不等式组$\left\{\begin{array}{l}{x+2≥a}\\{1-x≥2a}\end{array}\right.$得:a≤1.
∴a的取值可以为0,1.
P=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了概率公式、解一元一次不等式组、抛物线与x轴的交点,解题的关键是解关于a的不等式组,得出a的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据抛物线与x轴没有交点得出关于a的一元二次不等式组是关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.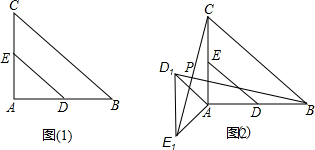 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.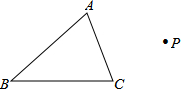 如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.
如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.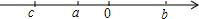 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.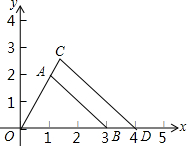 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.